(O3) Finding Absolute Extrema#

By the end of the lesson you will be able to:

  • use the Closed Interval Method to find the absolute maximum and absolute minimum values of a continuous function on a closed interval.

  • find the absolute extreme value of a continuous function with one critical number on on an open interval.

Lecture Videos#

Definitions#

Relative Maximum / Minimum

A local maximum value of \(f\) is a number \(f(c)\) such that \(f(c)\geq f(x)\) for \(x\) near \(c\).

A local minimum value of \(f\) is a number \(f(c)\) such that \(f(c)\leq f(x)\) for \(x\) near \(c\).

Absolute Maximum / Minimum

The absolute maximum value of \(f\) is a number \(f(c)\) such that \(f(c)\geq f(x)\) for all \(x\) in the domain of \(f\).

The absolute minimum value of \(f\) is a number \(f(c)\) such that \(f(c)\leq f(x)\) for all \(x\) in the domain of \(f\).

Extreme Value Theorem#

Extreme Value Theorem

If \(f\) is a continuous function on a closed interval \([a,b]\), then \(f\) is guaranteed to have an absolute maximum value and an absolute minimum value somewhere on that interval.

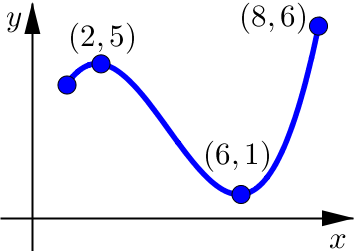
Graph of a continuous function

In this graph we see that the function is:

  • Defined on \([1,8]\) which is a closed interval.

  • Continuous on the closed interval \([1,8]\).

    • no jumps, breaks, or holes

  • Absolute Maximum at \(x=8\) with Value \(=6\).

  • Absolute Minumum at \(x=6\) with Value \(=1\).

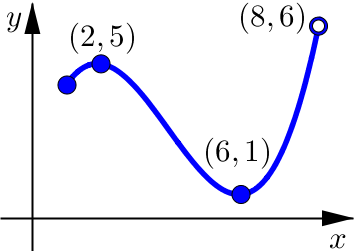
Graph of a discontinuous function

In this graph we see that the function is:

  • Defined on \([1,8)\) which is not a closed interval.

    • does not contain both endpoints

  • Continuous on the interval \([1,8)\).

    • no jumps, breaks, or holes

  • Absolute Maximum None.

  • Absolute Minumum at \(x=6\) with Value \(=1\).

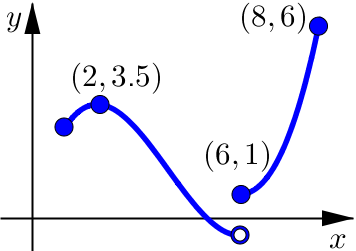
Graph of a discontinuous function

In this graph we see that the function is:

  • Defined on \([1,8]\) which is a closed interval.

  • Discontinuous on the interval \([1,8]\) (jumps at \(x=6\)).

  • Absolute Maximum at \(x=8\) with Value \(=6\).

  • Absolute Minumum None.

After looking at these graphs, we see that for the Extreme Value Theorem to work, we really do need both:

  • function \(f\) to be defined on a closed interval

  • function \(f\) to be continuous on this closed interval.

Critical Numbers#

Fermat’s Theorem

If \(f\) has a local maximum or minimum at \(x=c\), then either:

\[ f'(c)=0 \qquad \text{or}\qquad f'(c) \text{ DNE} \]

Critical Numbers

The number \(x=c\) is a critical number of \(f\) provided either:

\[ f'(c)=0 \qquad \text{or}\qquad f'(c) \text{ DNE} \]

and \(c\) is in the domain of \(f\).

Critical Number with zero derivative and local min

In this graph we see that the function has a:

  • Local Minimum at \(x=c\).

  • Critical Number at \(x=c\) since \(f'(c)=0\)

Note that since the derivative is zero at \(x=c\) we are seeing a more “rounded” shape to our graph at this local minimum. The graph smoothly switches from decreasing to increasing and where this happens it temporarily flattens out.

Critical number with nondifferentiable point and local min

In this graph we see that the function has a:

  • Local Minimum at \(x=c\).

  • Critical Number at \(x=c\) since \(f'(c) \text{ DNE}\)

Note that since the derivative is undefined at \(x=c\) we are seeing a more drastic, abrupt, and “sharp” shape to our graph at this local minimum. The graph abruptly switches from decreasing to increasing and does not termporarily flatten out in the middle.

Critical number with zero derivative and no local extrema

In this graph we see that the function:

  • Does not have a Local Maximum or Minimum at \(x=c\).

  • But it does have a Critical Number at \(x=c\) since \(f'(c)=0\).

Even though the graph temporarily flattens out at \(x=c\), we do not have a change from decreasing to increasing.

After looking at these graphs, we see that the critical numbers are useful because they give us a place to start looking for local extrema.

But unfortunately, as the third graph shows, not every critical number of \(f\) gives us a local maximum or minimum.

Finding Absolute Extrema#

Where to look

Absolute extrema (if they exist) must occur at either critical numbers or endpoints.

Remember:

  • Absolute Maximum Value is the largest value of \(f\)

  • Absolute Minimum Value is the smallest value of \(f\)

Closed Interval Method

  1. Verify that \(f\) is continuous on \([a,b]\).

  2. Find the critical numbers of \(f\) in the interval \((a,b)\).

  3. Evaluate \(f\) at the endpoints and critical numbers.

  4. Compare the resulting values:

    • the largest value is the Absolute Maximum Value

    • the smalles value is the Absolute Minumum Value

Example 1#

Find the absolute maximum and minimum values of:

\[ f(x) =x^3+3x^2-9x-7 \quad \text{on} \quad [-6,4] \]

Click through the tabs to see the steps of our solution.

Function \(f\) is a polynomial and is therefore continuous for all real numbers, but specifically it is continuous for all numbers in the closed interval \([-6,4]\).

  • continuous function? Yes.

  • closed interval? Yes.

Therefore, this function is guaranteed to have both an absolute maximum and absolute minimum on this interval.

In order to find the critical numbers, we first need to calculate the derivative and simplify it.

\[\begin{split} \begin{aligned} f'(x) & = 3x^2+6x-9 \\ & \\ & = 3(x^2+2x-3) \\ & \\ & = 3(x+3)(x-1) \\ \end{aligned} \end{split}\]

We factored the derivative in order to simplify it. This will make it easier to work with in some of our later steps.

Next we need to determine where the derivative is equal to \(0\), which we do by setting up the equation and solving for \(x\).

\[\begin{split} f'(x) = 0 & \xrightarrow{\text{set up}} 3(x+3)(x-1)=0 \\ & \\ & \xrightarrow{\text{set each factor} =0} (x+3) =0 \quad \text{or}\quad (x-1)=0\\ & \\ & \xrightarrow{\text{solve for } x} x=-3 \quad \text{or}\quad x=1\\ \end{split}\]

From here we see that \(f'(x)=0\) when \(x=-3\) and \(x=1\). (This is easy to do, because we factored our derivative earlier.)

Finally, we need to determine where the derivative is undefined. For a polynomial though, the derivative is always defined. So \(f'(x) \text{ DNE}\) does not happen for any \(x\)-values for this function.

Critical Numbers: Putting all of this together, we can say that this function has critical numbers \(x=-3\) and \(x=1\).

Next we need to evaluate the original function at the:

  • critical numbers: \(x=-3\) and \(x=1\)

  • and interval endpoints: \(x=-6\) and \(x=4\).

(Notice that we evaluate the original function \(f\), not its derivative \(f'\).)

Critical Numbers

\[\begin{split} \begin{aligned} f(-3) & = (-3)^3+3(-3)^2-9(-3)-7 & = 20 \\ f(1) & = (1)^3+3(1)^2-9(1)-7 & = -12 \\ \end{aligned} \end{split}\]

Endpoints

\[\begin{split} \begin{aligned} f(-6) & = (-6)^3+3(-6)^2-9(-6)-7 & = -61\\ f(4) & = (4)^3+3(4)^2-9(4)-7 & = 69\\ \end{aligned} \end{split}\]

Finally, we compare all of the values we found. The largest of these will be the Absolute Maximum Value and the smallest will be the Absolute Minimum Value.

\[\begin{split} \begin{aligned} f(-3) & = 20 \qquad \qquad & f(1) = -12 \\ && \\ f(-6) & = -61 \qquad \qquad& f(4) = 69 \\ \end{aligned} \end{split}\]

From these values we see:

  • Absolute Max Value is \(69\) which occurs at \(x=4\).

  • Absolute Min Value is \(-61\) which occurs at \(x=-6\).

Example 2#

Find the absolute maximum and minimum values of:

\[ f(x) =x^{1/3} (5-x) \quad \text{with} \quad -8\leq x\leq 1 \]

Function \(f\) is the continuous product of a root function with a polynomial. The interval \([-8,1]\) is a closed interval, since it contains both of its endpoints.

  • continuous function? Yes.

  • closed interval? Yes.

Therefore, this function is guaranteed to have both an absolute maximum and absolute minimum on this interval.

In order to find the critical numbers, we need to first calculate the derivative.

\[\begin{split} \begin{aligned} f'(x) & = \big[ x^{1/3} \big]' (5-x) + x^{1/3} \big[ 5-x \big]' \\ & \\ & = \tfrac{1}{3}x^{-2/3} (5-x) + x^{1/3} (-1) \\ \end{aligned} \end{split}\]

This is fine for just calculating the derivative, but we need to simplify this before trying to solve for the critical numbers.

\[\begin{split} \begin{aligned} f'(x) & = \dfrac{5-x}{3x^{2/3}}-x^{1/3} \\ & \\ & = \dfrac{5-x}{3x^{2/3}}-x^{1/3}\cdot\dfrac{3x^{2/3}}{3x^{2/3}} \\ & \\ & = \dfrac{5-x}{3x^{2/3}}-\dfrac{3x}{3x^{2/3}} \\ & \\ & = \dfrac{5-x-3x}{3x^{2/3}} \\ & \\ & = \dfrac{5-4x}{3x^{2/3}} \\ \end{aligned} \end{split}\]

Writing the derivative as a single fraction, is going to make finding the critical numbers much easier.

Since the derivative is written as a single fraction, we can find the critical numbers by looking at just the numerator and just the denominator:

\[\begin{split} \begin{aligned} f'(x) = 0 & \longrightarrow \text{set numerator } =0 \\ & \\ f'(x) \text{ DNE} & \longrightarrow \text{set denominator } =0 \\ \end{aligned} \end{split}\]

In order to find where the derivative is equal to \(0\), we start with our derivative (written as a single fraction), set the numerator equal to \(0\) and solve for \(x\).

\[ f'(x) = 0 \xrightarrow{\text{numerator} =0} 5-4x=0 \]

From here we see that \(f'(x)=0\) when \(x=5/4\).

In order to find where the derivative is undefined, we set the denominator equal to \(0\) and solve for \(x\).

\[ f'(x) \text{ DNE} \xrightarrow{\text{denominator} =0} 3x^{2/3}=0 \]

From here we see that \(f'(x) \text{ DNE}\) when \(x=0\).

Next we need to evaluate the original function \(f\) (not its derivative \(f'\)) at the:

  • critical numbers: \(\overbrace{x=0}^{\text{inside interval}}\) and \(\overbrace{x=5/4}^{\text{outside interval}}\)

  • and interval endpoints: \(x=-8\) and \(x=1\).

However, since we are trying to find the absolute extrema inside the interval \([-8,1]\), we do not need to consider the critical number \(x=5/4\), since this is outside of the interval.

Critical Numbers inside interval

\[\begin{split} \begin{aligned} f(0) & = (0)^{1/3} (5-0) & = 0 \\ \end{aligned} \end{split}\]

Endpoints of interval

\[\begin{split} \begin{aligned} f(-8) & = (-8)^{1/3} (5-(-8)) & = -26\\ && \\ f(1) & = (1)^{1/3} (5-1) & = 4\\ \end{aligned} \end{split}\]

Finally, we compare all of the values that we found. The largest of these will be the Absolute Maximum Value and the smallest will be the Absolute Minimum Value.

\[\begin{split} \begin{aligned} f(0) & = 0 & \\ && \\ f(-8) & = -26 \qquad \qquad& f(1) = 4 \\ \end{aligned} \end{split}\]

From these values we see:

  • Absolute Max Value is \(4\) which occurs at \(x=1\).

  • Absolute Min Value is \(-26\) which occurs at \(x=-8\).

Reminders

A few reminders about Critical Numbers and Terminology:

  • The Max / Min Value is the output of the function (we also usually state the \(x\)-value where this min/max occurs).

  • We only consider the critical numbers of the function that are inside the closed interval.

  • For a number \(x=c\) to be a critical number it needs to be in the domain of \(f\) (in addition to either \(f'(c)=0\) or \(f'(c)\) DNE)