(L6) Continuity#
By the end of the lesson you will be able to:
determine and explain why a function is continuous (or not)
Lecture Video#
Definition of Continuity#
Graphical Interpretation#
Continuity (intuitive definition)
A function is continuous provided its graph does not have any breaks or gaps.
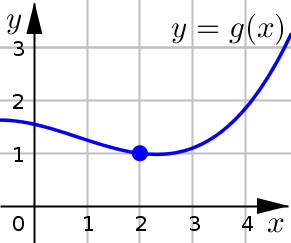
Why is this function continuous at \(x=2\)?
We see that there are not any breaks or gaps at \(x=2\). Specifically, the left-side limit is 1, the right-side limit is 1, and the actual function value is 1.
Intuitively, we can draw the graph of this function without taking our pen off the page at \(x=2\).
Limit Definition#
Continuity (limit definition)
A function \(f\) is continuous at \(x=a\) provided:
How do we check that a function is continuous at \(x=a\)?
Determine if \(f(a)\) is defined.
Calculate the limit: \(\displaystyle \lim_{x\to a}f(x)\)
This means calculate both the left side limit
And the right side limit
Show that these two values are equal. That is:
Example 1#
The given function is known to be continuous at \(x=1\). Use this to evaluate the following limit.
Solution and Explanation
Since we know this function is continuous at \(x=1\), the limit definition of continuity tells us that:
If we read this equation from left to right, it says that to actually calculate the limit, we simply need to plug \(x=1\) into the function and evaluate.
Done! Knowing that a function is continuous allows to quickly calculate any necessary limits.
Motivational Example
This example shows us why we are interested in determining the \(x\)-values where a function \(f\) is continuous.
Example 2#
Determine whether the functions, whose graphs are given below, are continuous at \(x=2\). Use the limit defintion in your work.
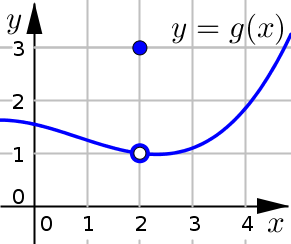
Solution and Explanation
Discontinuous at \(x=2\).
The function value and the limit are not equal at \(x=2\):
Function Value: \(g(2)=3\)
Limit: \(\displaystyle \lim_{x\to 2} g(x) =1\)
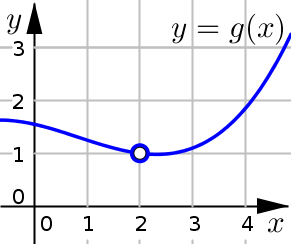
Solution and Explanation
Discontinuous at \(x=2\).
The function is undefined at \(x=2\).
Function Value: \(g(2)\) is undefined
Limit: \(\displaystyle \lim_{x\to 2} g(x) =1\)
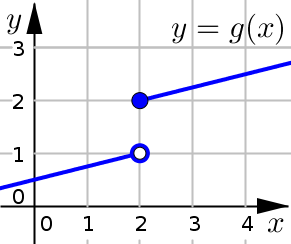
Solution and Explanation
Discontinuous at \(x=2\).
The limit does not exist at \(x=2\):
Function Value: \(g(2)=2\)
Left-Side Limit: \(\displaystyle \lim_{x\to 2^-} g(x) =1\)
Right-Side Limit: \(\displaystyle \lim_{x\to 2^+} g(x) =2\)
Overall Limit: \(\displaystyle \lim_{x\to 2} g(x) = \text{DNE}\)
Since the left and right side limits are not equal, the overall limit does not exist.
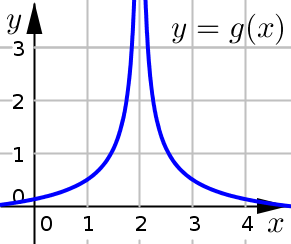
Solution and Explanation
Discontinuous at \(x=2\).
The function is undefined and the limit does not exist at \(x=2\):
Function Value: \(g(2)\) is undefined
Overall Limit: \(\displaystyle \lim_{x\to 2} g(x) =\infty\)
Since the overall limit is infinite, it technically does not exist.
Example 3#
Determine whether the following function is continuous at \(x=20\).
Click through the tabs to see the steps of our solution.
In order to determine if the function is continuous, we need to calculate the limit of the function as \(x\) approaches \(20\). In order to do this, we need to calculate both the left and right sided limits. Let’s start with the left.
Notice that left of \(x=20\) corresponds with the inequality \(x<20\) (smaller values). This will help us identify which piece to use for \(C(x)\):
Direct evaluation works in this last step since \((100+12x)\) is a polynomial.
Right of \(x=20\) corresponds with the inequality \(x>20\) (larger values), so we will need to use the other piece of our function’s definition here.
Direct evaluation was again helpful, since \((180+8x)\) is a polynomial.
So far we have shown that both the left and right sided limits exist and are equal to the same value of \(340\). This means that are overall limit exists as well:
So far so good for our continuity investigation!
Caution: Showing the limit exists is not enough to show continuity. We also need to show that the limit is equal to our function’s value here at \(x=20\).
To find the value, we just plug \(x=20\) into our function. But what piece should we use? If we look at the definition of \(C\), we see that one of the inequalities is \(x\leq 20\). This tells us we need to use this piece, namely \((100+12x)\).
So far we have shown that the limit exists and is given by:
We have also shown that the function is defined at \(x=20\) with value:
From this we see that these two values both exist and are equal:
Allowing us to conclude that function \(C\) is continuous at \(x=20\).
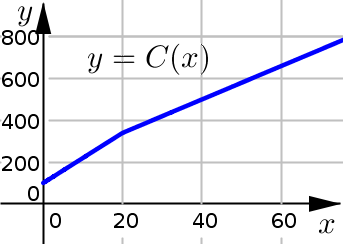
(Our conclusion does agree with the graph of the function - as there are not any jumps or breaks in the graph at \(x=20\).)
Example 4#
Determine whether the following function is continuous at \(x=3\).
Solution and Explanation
To determine the continuity of a function from the limit definition, there are a few things we need to check:
Evaluate the function directly at \(x=3\).
The limit of the function as \(x\to3\). (Both the left and right limits.)
Compare the results.
Usually evaluating the function is easiest, so we start with that. Let’s plug \(x=3\) into the function and see what we get:
which is undefined.
Since \(f(3)\) is undefined, it is not necessary to calculate the limit. We can immediately conclude that this function is not continuous at \(x=3\). Although it may be continuous at other \(x\)-values.
Example 5#
Determine whether the following function is continuous at \(x=3\).
Click through the tabs to see the steps of our solution.
To determine the continuity of a function from the limit definition, there are a few things we need to do:
Evaluate the function directly at \(x=3\)
Calculate the limit of the function as \(x\to3\). Both the left and right limits.
Compare the results. The values from steps 1 and 2 need to be equal.
Usually evaluating the function is easiest, so we start with that.
Let’s plug \(x=3\) into the function and see what we get.
Since this is a piece-wise function, we look for the piece where \(x=3\) and see what the function value should be. In this case it explicitly tells us. How nice!
Alright, so the function is defined at \(x=3\) and we know its value. The next step is to calculate the limit.
Since we have a piece-wise function, in order to calculate the left-side limit at \(x=3\), we need to determine which piece of the function we should use for \(x<3\) (left-side limit requires smaller \(x\)-values).
Since the two pieces of our function are defined on \(x\neq 3\) and \(x=3\), the \(x\neq 3\) piece includes the \(x<3\) condition for our left-side limit. So for \(x<3\) we have:
Now we’re ready to start the limit calculation. To give us a starting point for this calculation, let’s plug \(x=3\) in and see what we get:
This is not the answer (in fact it is undefined), but it does tell us something: we have a \(c/0\)-form. Which means the limit is infinite (either \(+\infty\) or \(-\infty\)).
To determine which it is, we need to use a test number that is close to 3 but slightly smaller:
Seeing how this is negative, we conclude:
At this point, we have enough information to make a decision about the continuity of this function at \(x=3\).
But for practice, you should try showing that for the right side limit we have:
Seeing how the left side limit is infinite, this also means that the (overall) limit does not exist.
Since the limit does not exist as \(x\) approaches \(3\), we conclude that this function is discontinuous at \(x=3\).
Continuity of Elementary Functions#
Theorem
All elementary functions listed on the table below are continuous on their domains.
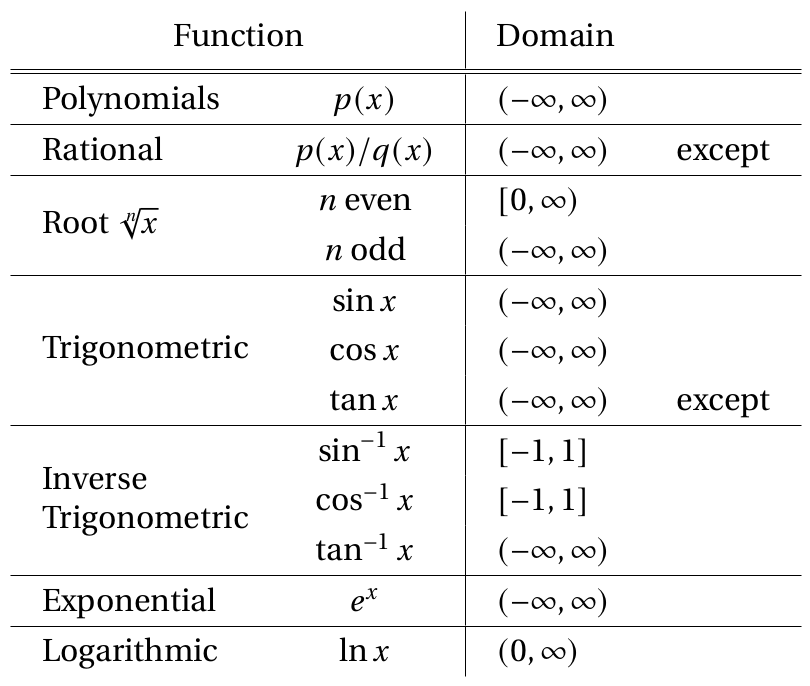
A few exceptions and comments
Rational functions are continuous except where the denonimator \(q(x)=0\).
\(\tan x\) is continuous except where \(\cos x=0\).
Even Roots are only defined for non-negative numbers.
Logarithms are only defined for postive numbers.
Example 6#
Calculate the following limit:
Click through the tabs to see the steps of our solution.
Since the function \(f(h)= \dfrac{h^2+2h+3}{4h+5}\) is a polynomial divided by a polynomial, we know that it is a rational function.
The domain of a rational function is all real numbers except where the denominator is \(0\). Let’s find where this happens!
We set \(4h+5\) equal to \(0\) and solve for \(h\), giving us \(h=-\tfrac{5}{4}\). This is the only real number not in the domain of this function:
Since this is a rational function and \(h=0\), the number we’re approaching, is in the domain, we can say that this function is continuous at \(h=0\).
Knowing this will allow us to calculate the desired limit by simply evaluating the function directly at \(h=0\).
Knowing that the function is continuous at \(h=0\), we calculate:
Done!
Arithmetic and Continuous Functions#
Theorem
If both: \(f\) is continuous at \(x=a\) and \(g\) is continuous at \(x=a\), then all of the following are continuous at \(x=a\) as well:
Essentially what this theorem tells us, is that doing arithmetic preserves continuity (except we need to be careful with division). So for instance, if we start with two continuous functions and then add them together, the brand new function we get is going to be continuous as well.
Example 7#
Determine where the following function is continuous.
Click through the tabs to see the steps of our solution.
We will start by determining the continuity for each distinct part of our function. To do this, it will be helpful to rewrite it is a product:
The first part of our function is \(3\ln x\), which is a constant multiple of the natural log function. Since \(\ln x \) is continuous on its domain. This means \(3\ln x\) is continuous there as well: for all \(x\)-values in the interval \((0,\infty)\)
Our next part is \(\tan^{-1}x\), which is an inverse trigonometric function. It therefore is continuous on its domain: \((-\infty,\infty)\).
Since \(3\ln x \) is continuous on \((0,\infty)\) and \(\tan^{-1}x\) is continuous on \((-\infty,\infty)\), when we add these two functions the result must also be continuous on \((0,\infty)\). Note that we can only use the numbers that appear in both sets.
Therefore, \(3\ln x+ \tan^{-1}x\) is continuous on \((0,\infty)\).
Another part of our function is the rational function \(\tfrac{1}{x^2-1}\). This function is defined everywhere except where the denominator is equal to \(0\), which happens at \(x=\pm 1\).
This rational function is therefore continuous on:
Putting it all together we know that:
In order to determine the domain of the product, we need to throw out any \(x\)-values that are not in both intervals. Doing this leaves us with:
And these are therefore the \(x\)-values where our function is continuous.
Example 8#
Calculate the following limit.
Click through the tabs to see the steps of our solution.
The easiest way to calculate this limit is by:
first showing that the function is continuous at \(x=\pi/2\) and then
using direct evaluation to calculate the limit.
Numerator: The function \(\sin x\) is a trig function, and so is continuous on its domain: \((-\infty, \infty)\).
Denominator: The function \(1+\cos x\) is the sum of two continuous functions, and so is continuous on its domain: \((-\infty, \infty)\).
Quotient: The only issue with doing the quotient is that we cannot divide by \(0\). So we need to determine where \(1+\cos x =0\), which happens at: \(x=\pm \pi, \pm 3\pi, \dots\).
Therefore, we see that our function is continuous on the interval \((-\infty, \infty)\) except at \(x=\pm \pi, \pm 3\pi, \dots\).
Most importantly though, we see that our function is continuous at \(x=\pi/2\).
Since we know that the function is continuous at the number we’re approaching, we can easily calculate the limit by direct evaluation:
Composition of Functions#
Composition
Given two functions \(f\) and \(g\), the composite function \(f\circ g\) is defined by:
Notes about composition:
In this definition, we sometimes call \(f\) the outer function and \(g\) the inner function.
The order does matter for composition. Usually \(f\circ g \neq g\circ f\).
For a little practice with composition, lets calculate \(f\circ u\) for:
Solution and Explanation
Continuous Outer Function#
Outer Function
If both: \(\displaystyle \lim_{x\to a} g(x)= b\) exists and \(f\) is continuous at \(x=b\) then,
Essentially, the way we can think of this result is that we can bring the limit inside the outer function, and calculate the limit of just the inner function. (The only condition for doing this is that the outer function needs to be continuous at whatever number we get for the inner limit.)
Example 9#
Calculate the limit:
Click through the tabs to see the steps of our solution.
Let’s start by calculating the limit of the inner function:
Plugging in directly, yields the indeterminate form \(\tfrac{0}{0}\), so we need to try an algebraic method. Because this involves a root function, we try using the conjugate method.
At the last step here, the reason we can evaluate this limit by direct evaluation is because it is continous at \(x=1\). Its the arithmetic combination of continuous functions with no division by \(0\) or negatives under the square root sign.
Our outer function is the inverse sine function, which we know is continuous on the interval \([-1,1]\).
Most importantly though (for this problem) is that we know it is continuous at \(x=1/2\).
Since we know that the outer function is continuous at the \(x=1/2\), we can bring the limit inside and calculate:
Composition of Continuous Functions#
Theorem
If both: \(g\) is continuous at \(x=a\) and \(f\) is continuous at \(g(a)\), then their composition \(f\circ g\) is continuous at \(x=a\).
Example 10#
Determine where the following functions are continuous:
(a) Function \(h(x)=(\sin x)^3\)
We need to start by identifying the outer and inner functions for this composite function. And then determine where they are continuous.
Outer Function: \(f(u)=u^3\) which is continuous on \((-\infty,\infty)\)
Inner Function: \(u(x)=\sin x\) which is continuous on \((-\infty,\infty)\)
Since the outer function does not have any restrictions, we see that the composite function \(h\) must also be continuous on \((-\infty,\infty)\).
(b) Function \(F(x)=\ln (1+\cos x)\)
We need to start by identifying the outer and inner functions for this composite function. And then determine where they are continuous.
Outer Function: \(f(u)=\ln u\) which is continuous on \((0,\infty)\)
Inner Function: \(u(x)=1+ \cos x\) which is continuous on \((-\infty,\infty)\)
However, the fact that natural log is only defined for positive numbers, puts some restriction on the inner function: we need \(1+\cos x>0\). Essentially we need to figure out where the inner function is positive, or alternatively, figure out where the inner function is either \(0\) or negative, and throw these \(x\)-values out.
Previously we’ve seen that \(1+\cos x=0\) for \(x=\pm \pi, \pm 3\pi, \dots\). Since \(\cos x\) never gets smaller than \(-1\), the sum \(1+\cos x\) never actually gets negative. The lowest it gets then is at those \(x\)-values, where the sum becomes \(0\).
Therefore, the composite function \(h\) must be continuous on the interval for the inner function \((-\infty,\infty)\) with \(x=\pm \pi, \pm 3\pi, \dots\) excluded. We can write this as:
Or we can write it as:
