(L5) Indeterminate Form (0/0)#
In this lesson, we will see how to:
calculate the limit of a function at a point using algebraic methods in the case where we have an indeterminate form.
Lecture Videos#
Example 4#
Compute the following limit:
Click through the tabs to see the steps of our solution.
Since we know that this is a rational function, let’s try plugging in \(x=2\) and see what we get:
The division by \(0\) tells us though, that \(x=2\) is not in the domain of our function. So direct evaluation does not work here.
Actually \(\tfrac{0}{0}\) is a very special type of limit which we call an indeterminate form. We will be spending a considerable amount of time investigating these forms.
Since we have the indeterminate form \(\tfrac{0}{0}\), one of our main strategies is factor and cancel: try to factor the numerator and denominator and look for any common factors that can cancel. Hopefully, this will get rid of the terms giving us those \(0\)’s in both the top and bottom of the fraction.
For this function, we can do a little factoring in the numerator:
Notice that there is an \((x-2)\)-factor that shows up in both the numerator and denominator. Canceling this gives us an easier limit to calculate:
As soon as we do the cancellation, we should try evaluating this new simplified limit.
(Note that direct evaluation works here, because \(x+2\) is a polynomial.) That’s it! There is the value for this limit.
Indeterminate Forms#
We have just encountered our first indeterminate form \(\dfrac{0}{0}\). As we saw in the last example when we encounter these, more work is required. We cannot determine the value of the limit just from the expression \(\tfrac{0}{0}\).
For intedeterminate forms, the limit could be infinite \(\infty\) or \(-\infty\), it might not exist (DNE), or it might be just some number. We don’t know until we do that additional work.
Note that while \(\tfrac{0}{0}\) is an indeterminate form, \(\tfrac{c}{0}\) is not. This usually gives us an infinite limit.
Canceling Variables#
Functions that are (almost) equal
If \(f(x)=g(x)\) except possibly at \(x=a\), then:
This theorem allows us to do what we did in the last example and cancel variable terms while calculating a limit. Let’s recall what we did there:
This is perfectly correct, because of the theorem above. Normally, canceling variable terms fundamentally changes a function - giving us something that is technically different. For limits though, this okay. We are not actually concerned with what happens directly at the number we are approaching, but rather what happens near this number.
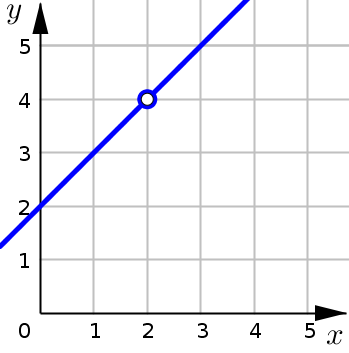
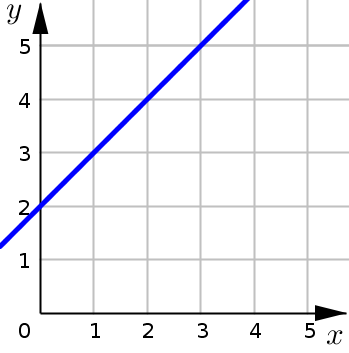
As we can see in the two graphs below, the functions \(\tfrac{(x+2)(x-2)}{x-2}\) and \(x+2\) are different. The fraction is undefined at \(x=2\), whereas \(x+2\) is defined everywhere. However, the limits of these two functions as \(x\) approaches \(2\) are equal. That is:
even though directly at \(x=2\) the functions themselves are not equal
their limits as \(x\) approaches \(2\) are equal:
Example 5#
Compute the following limit:
Warning
Here be Algebra tricks - Factor and Cancel
Click through the tabs to see the steps of our solution.
Since this is a rational function, let’s try plugging in \(h=0\) and see what we get:
The division by \(0\) tells us though, that \(x=5\) is not in the domain of our rational function. So direct evaluation does not work here.
Since we have this indeterminate form \(\tfrac{0}{0}\), we should look for any terms to factor and cancel.
Nothing immediately jumps out as being factorable, so we try simplifying the numerator first by multiplying out that squared term:
Using this in our limit and subtracting the \(25\)-terms, we get:
Now we have an expression that can be factored:
And canceling the common \(h\)-factor gives us:
As soon as we do the cancellation, it’s a good idea to try evaluating this new simplified limit.
That’s it! There is our answer. (Note that direct evaluation works here, because \(10+h\) is a polynomial.)
Example 6#
Compute the following limit:
Warning
Here be Algebra tricks - Rationalize
Click through the tabs to see the steps of our solution.
This isn’t a rational function nor a polynomial, but let’s try plugging in \(x=0\) anyway:
Since we have this indeterminate form \(\tfrac{0}{0}\), direct evaluation does not work here anyway, so we should look for terms to cancel.
When dealing with expressions involving root functions, one trick is to multiply by their conjugate term.
Here, the root expression is \(\sqrt{x+25}-5\) and its conjugate is \(\sqrt{x+25}+5\), which we find by switching the subtraction to addition (or vice versa if necessary). In order to eventually simplify our limit, we are going to mulitiply the numerator and denominator by this conjugate term:
We can do this, since we are effectively multplying by a fancy 1. Now, if we calculate the multiplication in the numerator we get:
Things simplify down quite nicely in the numerator!
We’re now ready to factor and cancel:
And canceling the common \(x\)-factor gives us:
As soon as we do the cancellation, it’s a good idea to try evaluating this new simplified limit.
That’s it!
Example 7#
Compute the following limit:
Warning
Here be Algebra tricks - Common Denominator
Click through the tabs to see the steps of our solution.
This is a rational function, so let’s try plugging in \(x=2\):
Direct evaluation does not work because of that division by \(0\), so we should look for some terms to cancel.
When dealing with two or more fractions, one helpful technique is to combine the fractions by finding the common denominator.
Let’s start by working with those two fractions in the numerator:
When we have fractions stacked on top of fractions like this, it can also be helpful to rewrite them as a product (rather than a quotient).
Looking for terms to cancel, we see that \((2-x)\) and \((x-2)\) are very similar.
Notice that \((2-x)=(-1)\cdot (x-2)\) which gives us:
And now we can cancel the common \((x-2)\)-factor, giving us:
As usual, as soon as we do the cancellation, the next step should be to try direct evaluation. If we get a number, well, that’ll be our answer.
Done! (Note that direct evaluation works here, because \(-\tfrac{1}{2x}\) is a rational function.)
Example 8#
Compute \(\displaystyle \lim_{x\to 20} f(x)\) where \(f\) is a piecewise-function given by:
Click through the tabs to see the steps of our solution.
In order to calculate this overall limit, we need to first calculate both of the one-sided limits. We usually need to do this for piecewise-functions if the limit we want to calculate happens to be near where the different pieces come together (in this case \(x=20\)).
Notice that left of \(x=20\) corresponds with the inequality \(x<20\) (smaller values). This will help us identify which piece to use for \(f(x)\):
Direct evaluation works in this last step since \((100+12x)\) is a polynomial.
Right of \(x=20\) corresponds with the inequality \(x>20\) (larger values), so we will need to use the square root piece of our function.
Notice that we had to use the Power Limit Law first. This allowed us to bring the limit inside the square root, which then allowed us to use direct evaluation on the polynomial \(180-4x\).
We calculated the left-sided limit:
and the right-sided limit:
Since these limits are different, we can conclude that the overall limit does not exist. That is:
(Remember that both the left and right sided limits need to be equal to each other in order for the overall limit to exist.)
