(O1) First Derivative Test#

By the end of the lesson you will be able to:

  • find all critical numbers of a function.

  • classify all critical numbers using the first derivative test.

Critical Numbers#

First Derivative Test#

Second Derivative Test#

Example 1#

Example 2#

Example 3#

One Critical Number#

Example 4#

Finding Local Extrema#

Fermat’s Theorem

If \(f\) has a local maximum or minimum at \(x=c\), then either \(f'(c)=0\) or \(f'(c) \; DNE\).

Critical Number

The number \(x=c\) is a critical number of \(f\) provided either:

\[ f'(c)=0 \qquad \text{or} \qquad f'(c) \;\text{ DNE} \]

and \(c\) is in the domain of \(f\).

Increasing
Flat
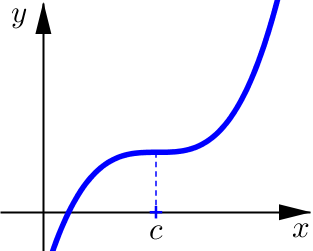
Decreasing

Classifying Critical Numbers#

First Derivative Test for Local Extrema

Let \(x=c\) be a critical number of continuous function \(f\).

  • If \(f'\) changes from \(+\) to \(-\) at \(c\), then \(f(c)\) is a local maximum.

  • If \(f'\) changes from \(-\) to \(+\) at \(c\), then \(f(c)\) is a local minimum.

  • If \(f'\) does not change signs at \(c\), then \(f(c)\) is not a local extremum.

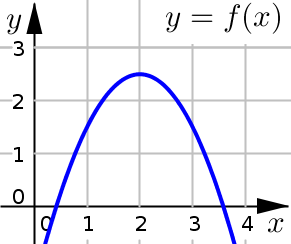
Increasing
Flat
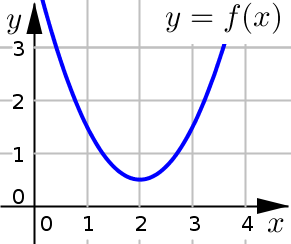
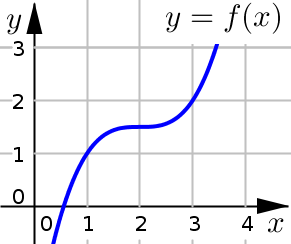
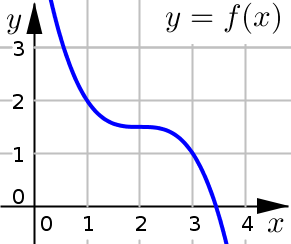
Decreasing
Decreasing

Example 1#

Function \(f\) is a function with domain \((-\infty, -3)\cup(-3,\infty)\) with first derivative given below. Find and classify all critical numbers of \(f\).

\[ f'(x)= x(x-1)^2(x+3)^{-3} \]

Example 2#

Find the local maximum and minimum values of:

\[ f(x)= \dfrac{1}{3}x^3-2x^2+3x+1 \]

Example 3#

Find the local maximum and minimum values of:

\[ f(x)= x^4-4x^3 \]

Example 4#

Find the local maximum and minimum values of:

\[ f(x)= \dfrac{2x^2}{x^2-1} \]

Example 5#

Find the local maximum and minimum values of:

\[ f(x)= xe^x \]