(DG5) Reading Graphs of Derivatives#
Given the graph of first derivative \(f'\) for some function \(f\), you will be able to:
locate the intervals of increase / decrease of \(f\).
locate the intervals of concavity of \(f\).
locate the local extrema of \(f\).
locate the inflection points of \(f\).
Given the graph of second derivative \(f''\) for some function \(f\), you will be able to:
locate the intervals of concavity of \(f\).
locate the inflection points of \(f\).
Lecture Videos#
Increasing / Decreasing#
Extreme Values#
Concavity#
Example 2#
First Derivative Rule#
Second Derivative Rule#
Examples 5 and 6#
Example 7#
First Derivative#
Increase / Decrease
For the interval \((a,b)\), if \(f\) is differentiable then:
\(f'(x)>0 \implies f\) is increasing
\(f'(x)<0 \implies f\) is decreasing
First Derivative Test for Local Extrema
Let \(x=c\) be a critical number of continuous function \(f\).
If \(f'\) changes from \(+\) to \(-\) at \(c\), then \(f(c)\) is a local maximum.
If \(f'\) changes from \(-\) to \(+\) at \(c\), then \(f(c)\) is a local minimum.
If \(f'\) does not change signs at \(c\), then \(f(c)\) is not a local extremum.
Second Derivative#
Concave up / Concave Down
For the interval \((a,b)\):
\(f''(x)>0 \implies f\) is concave up
\(f''(x)<0 \implies f\) is concave down
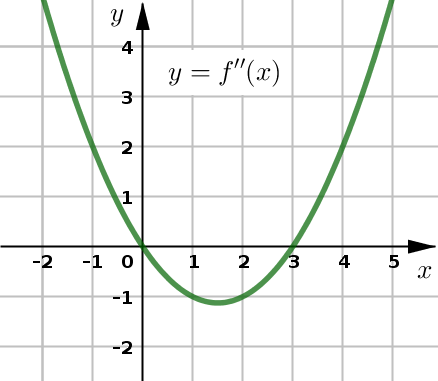
Example 1#
The graph of \(f''\) is given below for some function \(f\).
Find the open interval(s) where \(f\) is concave up / concave down.
Find the \(x\)-value(s) where \(f\) has an inflection point.
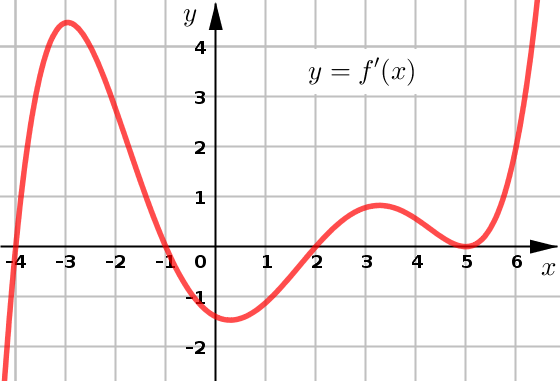
Example 2#
The graph of \(f'\) is given below for some function \(f\).
Find the open interval(s) where \(f\) is increasing / decreasing.
Find the critical number(s) of \(f\).
Classify the critical number(s) of \(f\) as either local maximum, local minimum, or neither.
Find the open interval(s) where \(f\) is concave up / concave down.
Find the \(x\)-value(s) where \(f\) has an inflection point.
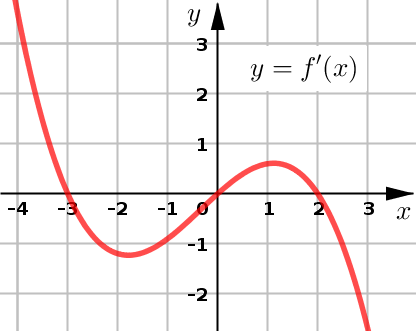
Example 3#
The graph of \(f'\) is given below for some function \(f\).
Find the open interval(s) where \(f\) is increasing / decreasing.
Find the critical number(s) of \(f\).
Classify the critical number(s) of \(f\) as either local maximum, local minimum, or neither.
Find the open interval(s) where \(f\) is concave up / concave down.
Find the \(x\)-value(s) where \(f\) has an inflection point.