(I1) Antiderivatives & Indefinite Integrals

By the end of the lesson you will be able to:

• calculate the indefinite integral of basic functions

• (These are integrals that can ultimately be solved using the sum, difference, or constant multiple rules in conjunction with our list of elementary forms).

Lecture Videos

Definition of Antiderivative

Constant \(+C\)

Definition of Indefinite Integral

Constant and Power Rule

Example 1

Sum and Constant-Multiple Rules

Example 4

Other Variables

Elementary Forms

Examples of Basic Integrals

---

Definition of Antiderivative

Antiderivative

A function \(F\) is an antiderivative of a function \(f\) if:

\[ F'(x)=f(x) \]

Many Antiderivatives

A function \(f\) can have more than one antiderivative. As an example, consider the function \(f(x)=x^2\).

Antiderivative \(F_1\)

The function \(F_1(x)=\tfrac{1}{3}x^3\) is an antiderivative of \(f(x)\) since:

\[ F_1'(x)=\bigg[ \tfrac{1}{3}x^3 \bigg]' = \tfrac{1}{3} \cdot 3x^2 = x^2 =f(x) \]

Antiderivative \(F_2\)

The function \(F_2(x)=\tfrac{1}{3}x^3 + 1\) is an antiderivative of \(f(x)\) as well, since:

\[ F_2'(x)=\bigg[ \tfrac{1}{3}x^3 +1 \bigg]' = \tfrac{1}{3} \cdot 3x^2 + 0 = x^2 =f(x) \]

---

Constant \(+C\)

Differ by a Constant

Suppose that \(F_1\) and \(F_2\) are two antiderivatives of a continuous function \(f\), then \(F_1(x)=F_2(x)+C\), where \(C\) is a constant.

This theorem shows that any two antiderivatives of a function differ only by a constant \(C\).

Because of this, we use \(F(x)+C\) to represent all antiderivatives of function\(f\).

Antiderivatives

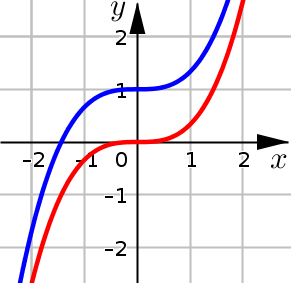
This graph shows two antiderivatives of \(f(x)=x^2\). Notice:

• Vertical Translation - These two graphs are vertical translations of each other: there is a constant distance of \(1\) between any two corresponding points on these graphs.

• Same Slope - These two graphs have the same slope at every corresponding point.

Parallel Lines

This graph shows two parallel lines. Notice:

• Vertical Translation - These two graphs are vertical translations of each other: there is a constant distance of \(1\) between any two corresponding points on these graphs.

• Same Slope - These two graphs have the same slope at every corresponding point.

---

Definition of Indefinite Integral

Indefinite Integral

Suppose that \(f(x)\) is a function whose antiderivatives are \(F(x)+C\). We write:

\[ \int f(x)\; dx = F(x)+C \]

In this notation, we call:

• \(\displaystyle \int\) the integral sign.

• function \(f(x)\), the integrand.

• \(dx\), the differential (which helps specify the variable)

Antiderivative

Think of the expression:

\[ \int \big[ \; \cdot \; \big]\; dx \]

as directions telling you to calculate the antiderivative of the function in between the brackets.

Derivative

Think of the expression:

\[ \dfrac{d}{dx} \big[ \; \cdot \; \big] \]

as directions telling you to calculate the derivative of the function in between the brackets.

Constant and Power Rule

Constant Rule

The antiderivative of a constant function (\(k\) constant) is:

\[ \int k \; dx = kx + C \]

Power Rule

The antiderivative of a power function is:

\[ \int x^n \; dx = \dfrac{1}{n+1} x^{n+1} + C \]

where \(n\) is any number except \(-1\).

Its important to note that the power rule only works for \(n\neq-1\). When the exponent is \(-1\), we need to use a different integration rule (which we’ll see a little later):

\[ \int x^{-1}\; dx = \int \dfrac{1}{x}\; dx \longrightarrow \text{Use log rule} \]

---

Example 1

Find the most general antiderivative of each of the following functions:

1. \(f(x)=5\)

2. \(f(x)= x^3\)

3. \(f(x)= \sqrt{x}\)

4. \(f(x)=\dfrac{1}{x^2}\)

Solution

Click through the tabs to see the solution for each part.

Note that when the directions say to find the most general antiderivative, we need to:

• calculate the indefinite integral of the function

• remember to include the \(+C\) at the end of our answer.

Part 1

Finding the most general antiderivative is equivalent to calculating the indefinite integral:

\[ \int 5 \; dx = 5x + C \]

Here we used the integral of a constant function formula, with \(k=5\):

Constant Function

\[ \int k \; dx = kx + C \]

Part 2

Again, finding the most general antiderivative is equivalent to calculating the indefinite integral:

\[ \int x^3 \; dx = \tfrac{1}{4}x^4 + C \]

Here we used the power rule formula, with \(n=3\):

Power Rule

\[ \int x^n \; dx = \tfrac{1}{n+1}x^{n+1} + C \]

Part 3

We begin by applying are usual strategy of rewriting a root function as a power function:

\[ \sqrt[n]{\; \cdot \;} \longrightarrow (\; \cdot \; )^{1/n} \]

And then to find the most general antiderivative we calculate the necessary indefinite integral.

\[ \int \sqrt{x} \; dx = \int x^{1/2} \; dx = \tfrac{2}{3}x^{3/2} + C \]

Here we used the power rule formula, with \(n=1/2\):

Power Rule

\[ \int x^n \; dx = \tfrac{1}{n+1}x^{n+1} + C \]

Part 4

We begin by applying are usual strategy of rewriting a fraction with negative exponents:

\[ \dfrac{1}{x^n} \longrightarrow x^{-n} \]

And then to find the most general antiderivative we calculate the necessary indefinite integral.

\[ \int \dfrac{1}{x^2} \; dx = \int x^{-2} \; dx = \tfrac{1}{-1}x^{-1} + C = -\dfrac{1}{x} + C \]

Here we used the power rule formula, with \(n=-2\):

Power Rule

\[ \int x^n \; dx = \tfrac{1}{n+1}x^{n+1} + C \]

---

Sum and Constant-Multiple Rules

The Constant-Multiple Rule

\[ \int k\cdot f(x) \, dx = k\cdot \int f(x) \, dx \]

The Sum / Difference Rule

\[ \int f(x) \pm g(x) \, dx = \int f(x) \, dx \pm \int g(x) \, dx \]

• The constant-multiple rule tells us that we can move the constant \(k\) outside and in front of the integration sign. Note that this only applies to constant-multiples. We cannot bring variables outside of the integration:

\[ \int x^3\cdot x^2 \, dx \neq x^3 \cdot \int x^2\, dx \]

• The sum / difference rule tells us that we can split up the integration wherever we see addition or subtraction signs.

Example 2

Evaluate the following indefinite integrals:

1. \(\displaystyle \int 2x^5 \; dx\)

2. \(\displaystyle \int \dfrac{4}{x^3} \; dx\)

3. \(\displaystyle \int 5\sqrt[3]{x} \; dx\)

Solution

Click through the tabs to see the solution for each part.

Note that when the directions say to calculate the indefinite integral, we need to:

• remember to include the \(+C\) at the end of our answer.

Part 1

We start by using the constant-multiple rule, with \(k=2\), to bring the \(2\) oustide of the integration:

\[ \int 2x^5 \; dx = 2\cdot \int x^5 \; dx \]

And then we use the power rule to integrate \(x^5\):

\[ = 2\big( \tfrac{1}{6}x^6 \big)+C \]

Constant-Multiple Rule

\[ \int k\cdot f(x) \, dx = k\cdot \int f(x) \, dx \]

Part 2

We start by using the constant-multiple rule, with \(k=4\), to bring the \(4\) oustide of the integration:

\[ \int \dfrac{4}{x^3} \; dx = 4\cdot \int \dfrac{1}{x^3} \; dx \]

Then we rewrite the fraction using a negative exponent and apply the power rule to finish integrating:

\[ 4\cdot \int x^{-3} \; dx = 4\big( \tfrac{1}{-2}x^{-2} \big)+C = -\dfrac{2}{x^2}+C \]

Constant-Multiple Rule

\[ \int k\cdot f(x) \, dx = k\cdot \int f(x) \, dx \]

Part 3

We start by using the constant-multiple rule, with \(k=5\), to bring the \(5\) oustide of the integration:

\[ \int 5 \sqrt[3]{x} \; dx = 5\cdot \int \sqrt[3]{x} \; dx \]

Then we rewrite the root sign using a fractional exponent and apply the power rule to finish integrating:

\[ 5\cdot \int x^{1/3} \; dx = 5\big( \tfrac{3}{4}x^{4/3} \big)+C = \tfrac{15}{4}x^{4/3}+C \]

Example 3

Evaluate the following indefinite integral:

\[ \int \big( 2x^7 +6x +5 \big) \; dx \]

Solution

Click through the tabs to see the steps of our solution.

Note that when the directions say to calculate the indefinite integral, we need to:

• remember to include the \(+C\) at the end of our answer.

Sum Rule

We begin by applying the sum rule to split up the integral into 3 separate integrals:

\[ \int \big( 2x^7 +6x +5 \big) \; dx = \int 2x^7 \; dx + \int 6x \; dx + \int 5 \; dx \]

The Sum / Difference Rule

\[ \int f(x) \pm g(x) \, dx = \int f(x) \, dx \pm \int g(x) \, dx \]

Constant-Multiple Rule

Next we apply the constant-multiple rule (twice) with \(k=2\) and \(k=6\) to bring those constants in front of the integral sign:

\[ \int 2x^7 \; dx + \int 6x \; dx + \int 5 \; dx = 2\cdot \int x^7 \; dx + 6\cdot \int x \; dx + \int 5 \; dx \]

Constant-Multiple Rule

\[ \int k\cdot f(x) \, dx = k\cdot \int f(x) \, dx \]

Basic Antideritvatives

Finally, use the power rule (twice) to calculate the first two integrals, and we use the constant-function formula to integrate the last term:

\[\begin{split} \begin{aligned} 2\cdot \int x^7 \; dx + 6\cdot \int x \; dx + \int 5 \; dx & = 2 \big( \tfrac{1}{8}x^{8} \big) + 6 \big( \tfrac{1}{2}x^{2} \big) + 5x+ C\\ & \\ & = \tfrac{1}{4}x^{8} + 3 x^{2} + 5x+ C\\ \end{aligned} \end{split}\]

Remember that \(+C\) at the end!

---

Example 4

Evaluate the following indefinite integrals:

1. \(\displaystyle \int \big( 2x^7 +6x + 5 \big) \; dx\)

2. \(\displaystyle \int \left(5x^4-\dfrac{4}{x^3} \right) \; dx\)

Solution

Click through the tabs to see the solution for each part.

Note that when the directions say to calculate the indefinite integral, we need to:

• remember the \(+C\) at the end of our answer.

Part 1

Once we are able to consistently calculate these indefinite integrals correctly, we don’t normally show the Sum/Difference or Constant-Multiple Rules in our work.

Let’s redo the previous example, showing the amount of work we normally show.

\[\begin{split} \begin{aligned} \int \big( 2x^7 +6x +5 \big) \; dx& = 2 \big( \tfrac{1}{8}x^{8} \big) + 6 \big( \tfrac{1}{2}x^{2} \big) + 5x+ C\\ & \\ & = \tfrac{1}{4}x^{8} + 3 x^{2} + 5x+ C\\ \end{aligned} \end{split}\]

And even that middle step might be too much. Once you really have the hang of these, you will most likely go from the integral right to the simplified answer. Remember \(+C\)!

Part 2

Let’s calculate this integral, showing the normal amount of work. The only step that we should show is rewriting the fraction using a negative exponent. It’s very easy to make a mistake with the power rule for negative exponents:

\[\begin{split} \begin{aligned} \int \left(5x^4-\dfrac{4}{x^3} \right) \; dx & = \int \left(5x^4-4 x^{-3} \right) \; dx\\ & \\ & = 5\cdot \big(\tfrac{1}{5}x^{5} \big) -4\cdot \big( \tfrac{1}{-2}x^{-2}\big)+ C\\ & \\ & = x^{5} +2x^{-2}+ C\\ \end{aligned} \end{split}\]

Other Variables

Sometimes we use variables other than \(x\) and \(y\), but the integration process is essentially the same. Just make sure you are consistent with the variable in your work.

\(x\)-variable

\[ \int x^2 \, dx = \tfrac{1}{3} x^3 + C \]

\(t\)-variable

\[ \int t^2 \, dt = \tfrac{1}{3} t^3 + C \]

Note that the differential (in this case \(dx\) or \(dt\)) tells us what variable we are integrating with respect to.

---

Elementary Forms

Any of the following integral formulas can be determined from our table of elementary derivatives. For instance, we know the following derivative:

\[ \dfrac{d}{dx}\big[ \sin x \big] = \cos x \]

If we read this backwards, it’s really telling us that the antiderivative of \(\cos x\) is \(\sin x\), that is:

\[ \int \cos x \; dx = \sin x+C \]

When we look at the derivative formulas:

\[ \dfrac{d}{dx}\big[ \underbrace{\sin x }_{\text{antiderivative}}\big] = \underbrace{\cos x}_{\text{derivative}} \]

Integral Formulas

\[\begin{split} \begin{array}{ l l l } & \displaystyle\int k \; dx = k x +C \qquad & \\ & & \\ & \displaystyle\int x^n \; dx = \dfrac{1}{n+1}x^{n+1} +C \qquad & \displaystyle\int \dfrac{1}{x} \; dx = \ln |x| +C \\ & & \\ & \displaystyle\int e^x \; dx = e^x +C \qquad & \displaystyle\int b^x \, dx = \dfrac{b^x}{\ln b} +C \\ & & \\ & \displaystyle\int \sin x \; dx = - \cos x +C \qquad & \displaystyle\int \cos x\; dx = \sin x+C \\ & & \\ & \displaystyle\int \sec^2 x \; dx = \tan x +C \qquad & \displaystyle\int \csc^2 x\; dx = - \cot x+C \\ & & \\ & \displaystyle\int \sec x \tan x\; dx = \sec x +C \qquad & \displaystyle\int \csc x \cot x\; dx = - \csc x+C \\ & & \\ & \displaystyle\int \dfrac{1}{1+x^2} \; dx = \tan^{-1} x +C \qquad & \displaystyle\int \dfrac{1}{\sqrt{1-x^2}} \; dx = \sin^{-1} x+C \\ \end{array} \end{split}\]

Domain of Antiderivative

When we are finding the antiderivative of a function, we want the domain of the function and its antiderivative to at least match (the domain of the antiderivative can be larger if needed).

The is why for we use \(\ln |x|\) with the absolute value as the antiderivative of \(\dfrac{1}{x}\). The domain of these two functions are the same: all real numbers \(x\neq 0\).

---

Examples of Basic Integrals

Calculate each of the following integrals:

1. \(\displaystyle \int \big( 2\sin x +3 \sec^2 x \big) \; dx\)

2. \(\displaystyle \int \left( \dfrac{\cos \theta}{\sin^2\theta} + \dfrac{5}{1+\theta^2} \right) \; d\theta\)

3. \(\displaystyle \int \big( 5e^x + x\sqrt{x} \big) \; dx\)

4. \(\displaystyle \int \left( \dfrac{t^2+1}{t} +3 \cos t \right) \; dt\)

Solution

Click through the tabs to see the solution for each part.

Note that when the directions say to calculate the indefinite integral, we need to:

• remember the \(+C\) at the end of our answer.

Part 1

In this integral we see \(\sin x\) and \(\sec^2 x\), so we look up (or have memorized) the corresponding antiderivatives on our table of elementary forms:

\[\begin{split} \begin{aligned} \int \big( 2\sin x +3 \sec^2 x \big) \; dx & = 2 \big( -\cos x \big) + 3 \big( \tan x \big) + C\\ & \\ & =-2 \cos x +3 \tan x + C\\ \end{aligned} \end{split}\]

Remember \(+C\) at the end for indefinite integrals!

Part 2

In this integral, the first fraction we have is not directly one of our elementary forms, so we try using trigonometric identities to rewrite this in one of these forms:

\[ \dfrac{\cos \theta}{\sin^2\theta} = \dfrac{1}{\sin\theta}\cdot \dfrac{\cos \theta}{\sin\theta} = \csc\theta \cot \theta \]

Now that we have an elementary form we can start the integration:

\[\begin{split} \begin{aligned} \int \left( \dfrac{\cos \theta}{\sin^2\theta} + \dfrac{5}{1+\theta^2} \right) \; d\theta & = \int \left( \csc\theta \cot \theta + 5\cdot \dfrac{1}{1+\theta^2} \right) \; d\theta\\ & \\ & = -\csc\theta +5\cdot \arctan \theta+ C\\ \end{aligned} \end{split}\]

Part 3

In this integral, the first term is a product of two variable terms, which we need to simplify first before integrating. So we do the multiplication.

Note that the only integration rules we have seen so far are for addition, subtraction, and constant-multiplication. We actually haven’t seen a rule on how to handle the multiplication of two variable terms.

\[ x\sqrt{x} = x\cdot x^{1/2} = x^{1+1/2} = x^{3/2} \]

Now that we have an elementary form (power function) we can start the integration:

\[\begin{split} \begin{aligned} \int \big( 5e^x + x\sqrt{x} \big) \; dx & = \int \big( 5e^x + x^{3/2} \big) \; dx \\ & \\ & = 5\cdot \big( e^x\big) + \tfrac{2}{5}x^{5/2}+ C\\ \end{aligned} \end{split}\]

Part 4

In this integral, the first term is a quotient of two variable terms, which we need to simplify first before integrating. So we do the division. (Note that we do not have a integral rule for fractions like this.)

\[ \dfrac{t^2+1}{t} = \dfrac{t^2}{t} + \dfrac{1}{t} = t + \dfrac{1}{t} \]

Now that we have an elementary form (sum of two power functions) we can start the integration:

\[\begin{split} \begin{aligned} \int \left( \dfrac{t^2+1}{t} +3 \cos t \right) \; dt & = \int \left( t + \dfrac{1}{t} +3 \cos t \right) \; dt \\ & \\ & = \tfrac{1}{2}t^{2} + \ln |t| + 3\sin t+ C\\ \end{aligned} \end{split}\]

Remember the \(+C\) and the absolute value sign.