(L2) Numerical Limits#
By the end of the lesson you will be able to:
find the one-sided limits of a function using numerical methods.
use the one-sided limits to determine the (overall) limit of a function using numerical methods.
Lecture Video#
Numerical Limits#
So far, we have seen how to use a graph to determine the behavior of a function near \(x=a\). We can also investigate this behavior with numerical methods using a table of \(x\)-values and the corresponding function values \(f(x)\).
Left-Sided Limits#
Remember that for left-sided limits we need to use \(x\)-values that are close to \(a\) but slightly smaller.
What is a list of \(x\)-values we could use to investigate \(x\to 2^-\) numerically?
\(x\) |
|---|
\(1.9\) |
\(1.99\) |
\(1.999\) |
\(1.9999\) |
Right-Sided Limits#
With right-sided limits we need to use \(x\)-values that are close to \(a\) but slightly larger.
What is a list of \(x\)-values we could use to investigate \(x\to 2^+\) numerically?
\(x\) |
|---|
\(2.1\) |
\(2.01\) |
\(2.001\) |
\(2.0001\) |
Example 3#
Compute the following limit numerically:
Click to go through the steps
Left-Sided Limit: Pick a list of \(x\)-values that are getting closer and closer to the number \(2\) (but are all slightly smaller).
Plug these numbers into the function \(f(x)=3x-5\) and record each of the outputs in a table, like below:
\(x\) |
\(f(x)\) |
|---|---|
\(1.9\) |
\(0.7\) |
\(1.99\) |
\(0.97\) |
\(1.999\) |
\(0.997\) |
\(1.9999\) |
\(0.9997\) |
From this table we see that as the input \(x\)-values get closer to the number \(2\) from the left, the output \(f(x)\)-values appear to be getting closer to the number \(1\). Therefore, we say:
Right-Sided Limit: Pick a list of \(x\)-values that are getting closer and closer to the number \(2\) (but are all slightly larger).
Plug these numbers into the function \(f(x)=3x-5\) and record each of the outputs.
\(x\) |
\(f(x)\) |
|---|---|
\(2.1\) |
\(1.3\) |
\(2.01\) |
\(1.03\) |
\(2.001\) |
\(1.003\) |
\(2.0001\) |
\(1.0003\) |
From this table we see that as the input \(x\)-values get closer to the number \(2\) from the right, the output \(f(x)\)-values appear to be getting closer to the number \(1\). Therefore, we say:
Since the left and right sided limits are both equal to the number \(1\) we conclude the overall limit is also equal to \(1\) as \(x\) approaches \(2\).
Example 4#
Compute the following limit numerically:
Click to go through the steps
Left-Sided Limit: Pick a list of \(x\)-values that are getting closer and closer to the number \(-3\) (but are all slightly smaller).
Plug these numbers into the function \(f(x)=\tfrac{3+x}{9-x^2}\) and record each of the outputs in a table, like below:
\(x\) |
\(f(x)\) |
|---|---|
\(-3.1\) |
\(0.1639344\) |
\(-3.01\) |
\(0.1663894\) |
\(-3.001\) |
\(0.1666389\) |
\(-3.0001\) |
\(0.1666639\) |
From this table we see that as the input \(x\)-values get closer to the number \(-3\) from the left, the output \(f(x)\)-values appear to be getting closer to the number \(0.1\overline{6}\). Therefore, we say:
Right-Sided Limit: Pick a list of \(x\)-values that are getting closer and closer to the number \(-3\) (but are all slightly larger).
Plug these numbers into the function \(f(x)=\tfrac{3+x}{9-x^2}\) and record each of the outputs in a table, like below:
\(x\) |
\(f(x)\) |
|---|---|
\(-2.9\) |
\(0.1694915\) |
\(-2.99\) |
\(0.1669449\) |
\(-2.999\) |
\(0.1666944\) |
\(-2.9999\) |
\(0.1666694\) |
From this table we see that as the input \(x\)-values get closer to the number \(-3\) from the right, the output \(f(x)\)-values appear to be getting closer to the number \(0.1\overline{6}\). Therefore, we say:
Since the left and right sided limits are both equal to the number \(0.1\overline{6}\) we conclude the overall limit is also equal to \(0.1\overline{6}\) as \(x\) approaches \(-3\).
Numerical Issues#
Estimates: The main issue with these graphical and numerical methods for calculating a limit is that they are both technically estimates. They give us a way to estimate the value of a limit (we’ll see how to calculate them exactly using algebraic methods).
False Positive: One of the issues we might encounter is a false positive. This can happen by just choosing unlucky input values to plug-in. As we can see in the graph below, if we had had the misfortune of picking all the \(x\)-values where the function crosses the horizontal axis, we might be tempted to conclude that \(\displaystyle \lim_{x\to0^+} f(x) =0\).
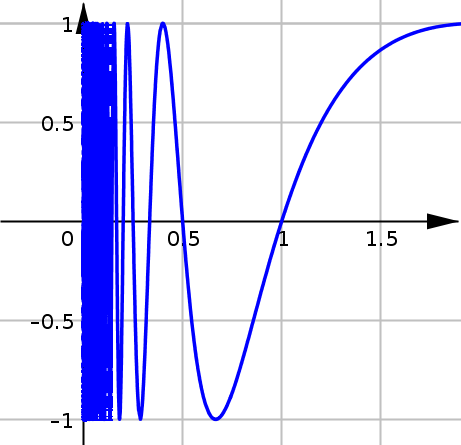
However someone else may have picked all the \(x\)-values where the function has a maximum value of \(1\), and a third person may have picked all the \(x\)-values where the function has its minimum value of \(-1\).
In fact this limit\(\displaystyle \lim_{x\to0^+} f(x)\) does not exist because as \(x\) gets closer to \(0\) from the right, the function bounces back and forth and repeatedly takes on all values between \(-1\) and \(1\).
Rounding: Also, whenever we evaluate a function, there is always the possibility of introducing rounding error which can have a significant impact on our calculations. Consider the following limit.
When numerically calculating this limit as \(x\) goes to \(0\), we would want to use input numbers that are close to \(0\). However, for this function here we actually reach a point where rounding error becomes an issue.
\(x\) |
\(f(x)\) |
|---|---|
\(0.1\) |
\(0.166662\) |
\(0.01\) |
\(0.166666\) |
\(0.001\) |
\(0.166666\) |
\(0.0001\) |
\(0.166666\) |
\(0.00001\) |
\(0.166671\) |
\(0.000001\) |
\(0.166979\) |
\(0.0000001\) |
\(0\) |
\(0.00000001\) |
\(0\) |
Plugging \(0.0000001\) directly into the function would apparently give us \(0\) as seen in this calculation from Google Calculator. But in actuality this is not possible, the only two places where this function is exactly equal to \(0\) is at \(x=-3\) and \(x=3\).