(L7) Limits at Infinity

By the end of the lesson you will be able to:

• find the limit of a function at infinity using graphical, numerical, and algebraic methods.

• find any horizontal asymptotes of a function.

Review Video

---

Limits at Infinity

Introduction

So far in our investigation of functions we have calculated limits where our input values \(x\) were approaching a specific number: something like \(x\to 2\) or \(x\to 0^+\).

If we look at the \(x\)-axis though, we might notice that there are two other directions to consider:

• the left end, where we move further and further to the left along the \(x\)-axis.

• the right end, where we move further to the right.

We call these two directions: limits at infinity.

Definitions

Finite Limit at Infinity

As input values, \(x\), get very large positive, the output values, \(f(x)\), get very close to number \(L\).

\[ \lim_{x\to\infty}f(x)=L \]

Infinite Limit at Infinity

As input values, \(x\), get very large positive, the output values, \(f(x)\), get very large positive.

\[ \lim_{x\to\infty}f(x)=\infty \]

Negative Infinite Limit at Infinity

As input values, \(x\), get very large positive, the output values, \(f(x)\), get very large negative.

\[ \lim_{x\to\infty}f(x)=-\infty \]

Right-End Behavior: In each of these limits, we are using the notation \(x\to\infty\) to denote that we are calculating the limit as input \(x\) gets very large positive.

Left-End Behavior: There are 3 similar definitions for the other direction as well. In this case though, we would use the notation \(x\to-\infty\) to denote that we are calculating the limit as input \(x\) gets very large negative.

---

Numerical Example

Let’s look at a little numerical example, to see how these different defintions work. In the table below, we see the values for 3 different functions \(f\), \(g\), and \(h\).

First Column

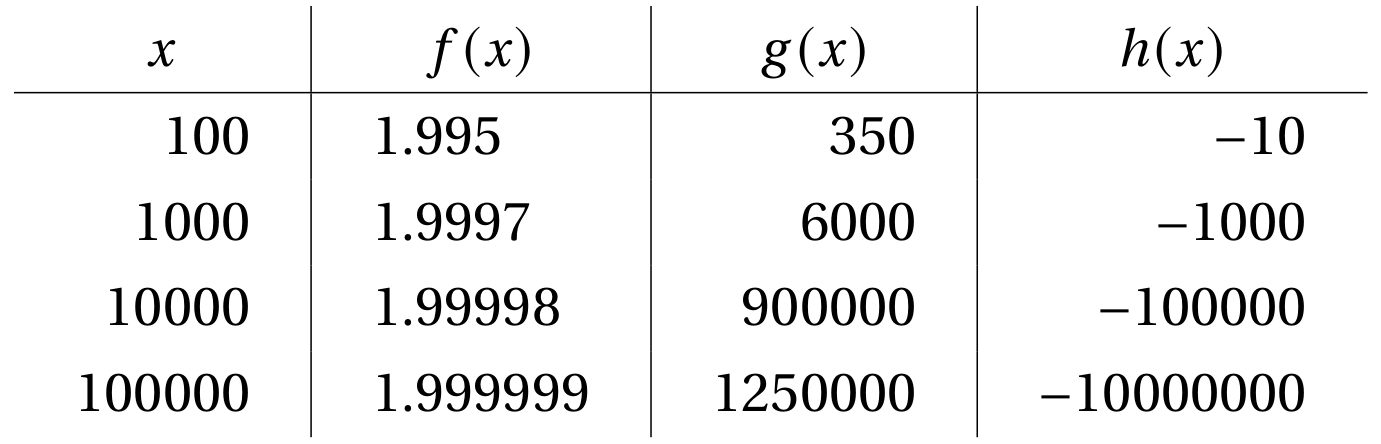
The first column shows us a few different input values, \(x\). As we read down this column, we see that these input values are getting large positive - telling us that we are going to be consider the limit at infinity where \(x\to\infty\).

Second

The second column has the corresponding function values for \(f\). As we read down this column, we see that these output values are getting closer and closer to the number \(2\). In this case we would write:

\[ \lim_{x\to\infty}f(x)=2 \]

Third

The third column has the corresponding function values for \(g\). As we read down this column, we see that these output values are getting larger and larger positive. In this case we would write:

\[ \lim_{x\to\infty}g(x)=\infty \]

Fourth

The fourth column has the corresponding function values for \(h\). As we read down this column, we see that these output values are getting larger and larger negative. In this case we would write:

\[ \lim_{x\to\infty}h(x)=-\infty \]

Horizontal Asymptotes

Horizontal Asymptotes

The horizontal line \(y=L\) is called a horizontal asymptote of the curve \(y=f(x)\) provided either (or both):

\[ \lim_{x\to -\infty}f(x)=L\qquad \text{or}\qquad \lim_{x\to \infty}f(x)=L \]

Note: To find all horizontal asymptotes, you need to check both limits at infinity.

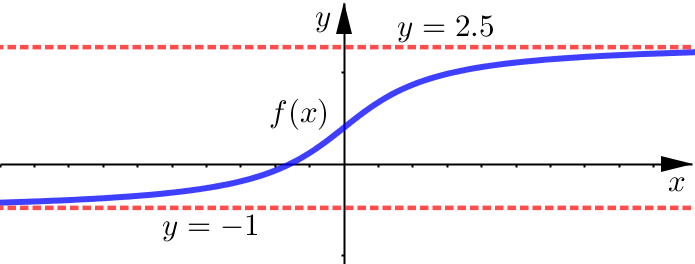
What are the horizontal asymptotes for this function?

This graph is an example of a function that has two distinct horizontal asymptotes: lines \(y=-1\) and \(y=2.5\).

• Left-end behavior is given by \(\displaystyle \lim_{x\to-\infty} f(x) = -1\)

• Right-end behavior is given by \(\displaystyle \lim_{x\to\infty} f(x) = 2.5\)

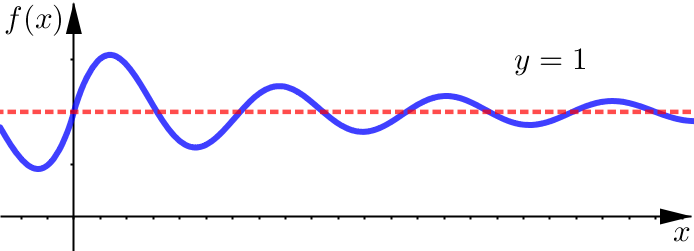
What are the horizontal asymptotes for this function?

This graph shows a function that has horizontal asymptote: line \(y=1\). We have enough information to say that the:

• Right-end behavior is given by \(\displaystyle \lim_{x\to\infty} f(x) = 1\)

Note that the function does oscillate around this line, but the amplitude is decreasing. So as the \(x\) values get large positive, the corresponding function values, \(f(x)\), do approach \(1\).

Basic Limits at Infinity

For our discusssion of the basic limits at infinity for power functions we will be looking at functions of the form: \(x^n\), \(1/x^n\), and \(x^{1/n}\). In each of these we’ll be using the convention that \(n\) is a positive integer.

Power Functions \(x^n\)

Let’s start with power functions of the form \(f(x)=x^n\) where \(n\) is a positive integer. (Actually, as we’ll next see with root functions, these results can be generalized so that \(n\) is a positive rational number. The only stipulation is that for the limit at negative infinity we cannot have an even root in our power function.)

Left End

\[\begin{split} \lim_{x\to -\infty}x^n = \begin{cases} \infty & \quad \text{n even} \\ - \infty & \quad \text{n odd} \\ \end{cases} \end{split}\]

Right End

\[ \lim_{x\to \infty}x^n = \infty \]

Below we see two examples of what the power function \(f(x)=x^n\) looks like graphically. The two different cases here are based on whether the exponent \(n\) is even or odd. All power functions of this form have either one of these two shapes.

Even Power

Odd Power

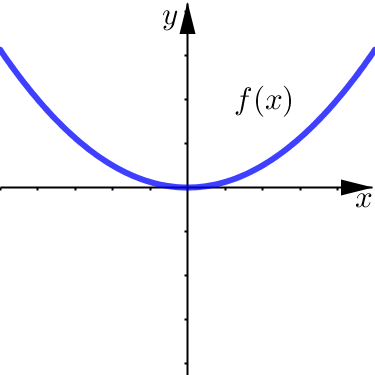
Notice that in each of these, there are no horizontal asymptotes.

---

Power Functions \(x^{1/n}\)

The end-behavior for power functions of the form \(f(x)=x^{1/n}\) (root functions) is very similar to the end-behavior of \(x^n\). The difference here is that we cannot calculate the even root of a negative number. So it does not make sense to actaully consider the limit as \(x\) gets large negative for even roots. Odd roots are perfectly fine though.

Left End

\[\begin{split} \lim_{x\to -\infty}x^{1/n} = \begin{cases} \text{undef.} & \; \text{n even} \\ - \infty & \; \text{n odd} \\ \end{cases} \end{split}\]

Right End

\[ \lim_{x\to \infty}x^{1/n} = \infty \]

Power Functions \(1/x^n\)

Next, we consider power functions of the form: \(f(x)=1/x^n\). Here, \(n\) can be a positive rational number, provided it makes sense: no limits at negative infinity for even root functions.

Left End

\[ \lim_{x\to -\infty}\dfrac{1}{x^n} = 0 \]

Right End

\[ \lim_{x\to \infty}\dfrac{1}{x^n} = 0 \]

Below we see two examples of what this power function, \(f(x)=1/x^n\), looks like graphically. Just as before, the two different cases here are based on whether the exponent \(n\) is even or odd - and we are guaranteed that it will be either one of these two shapes (for integer exponents).

Even Power

Odd Power

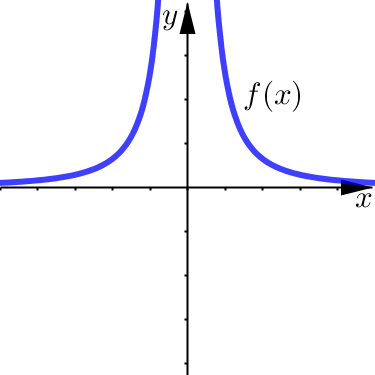
We have something interesting in both the left-end and right-end behavior here: our first concrete example of a horizontal asymptote. Because both limits are equal to \(0\), that means we have horizontal asymptote \(y=0\). You should be able to identify this line in the graphs below, noticing that our function appears to approach (in both directions) this horizontal line.

---

Constant Function

Limits at Infinity

\[ \lim_{x\to -\infty}k = k \qquad \lim_{x\to \infty}k = k \]

We can see that constant functions \(f(x)=k\) have horizontal asymptote \(y=k\) (occuring in both directions).

---

Exponential Functions

Limits at Infinity

\[ \lim_{x\to -\infty}e^x = 0 \qquad \lim_{x\to \infty}e^x = \infty \]

Similar limits exist for general exponential functions of the form \(b^x\) where base \(b\) is a number greater than \(1\).

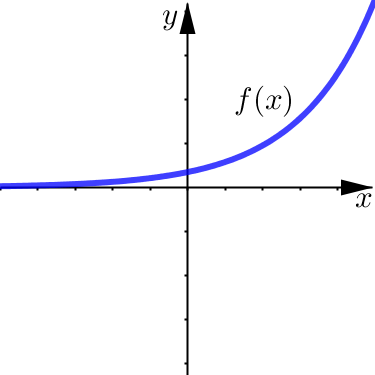
We can see that exponential functions \(f(x)=b^x\) have a horizontal asymptote \(y=0\), occuring in just the left-end direction.

---

Logarithmic Functions

Limits at Infinity

\[ \lim_{x\to -\infty}\ln |x| = \infty \qquad \lim_{x\to \infty} \ln |x| = \infty \]

If we consider the function \(\ln (x)\):

• the left-end limit is undefined. See note below.

• the right-end limit is the same as above.

Note: If we are only considering the function \(\ln(x)\), then the left-end limit is undefined. Natural log (or log functions in general), are only defined for positive numbers, so it does not actually make sense to consider the limit as \(x\) gets large negative for log functions without the absolute value.

Trigonometric Functions

In the information below, we have the limits at infinity explicitly listed for the sine function. However, the same results are true for all 6 trigonometric functions:

\[\begin{split} \sin x \qquad \cos x \qquad \tan x \\ \csc x \qquad \sec x \qquad \cot x \\ \end{split}\]

Limits at Infinity

\[ \lim_{x\to -\infty}\sin x = \text{DNE} \qquad \lim_{x\to \infty}\sin x = \text{DNE} \]

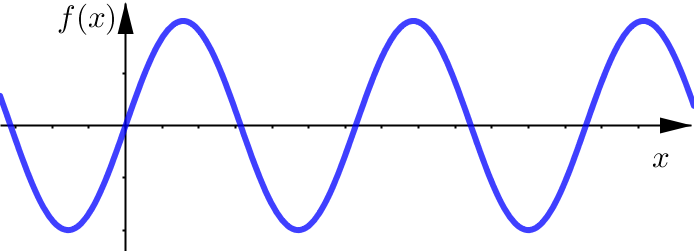
Looking at the graph of the sine function, we can see why these limits at infinity do not exist: the graph keeps oscillating back and forth with no decrease in amplitude.

Inverse Trigonometric Functions

The main inverse trigonometric function that we will be considering that actually has limits at infinity is \(\tan^{-1} x\) (the inverse tangent function).

Limits at Infinity

\[ \lim_{x\to -\infty}\tan^{-1} x = -\dfrac{\pi}{2}\qquad \lim_{x\to \infty}\tan^{-1} x = \dfrac{\pi}{2} \]

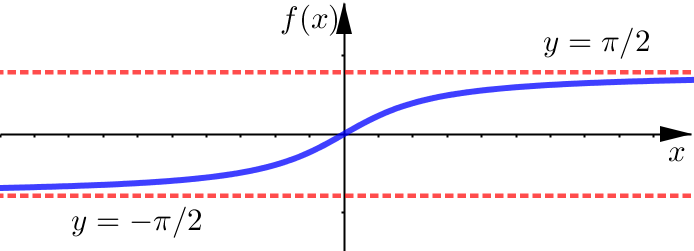
We can see that \(f(x)=\tan^{-1}x\) has two different horizontal asymptotes: \(y=\pi/2\) in the right-end direction and \(y=-\pi/2\) in the left-end direction.

Now you may be wondering: What about the other inverse trig functions? Technically, the inverse contangent function also has limits at infinity, but we will not be using that function too much in this course. As for inverse sine and inverse cosine, these functions are only defined on the finite interval \([-1,1]\) so it does not make sense to consider the limit as input \(x\) gets large positive or large negative.

---

Example 1

Compute the following limit at infinity:

\[ \lim_{x\to \infty} \dfrac{3x^2-x-2}{5x^2+4x+1} \]

Solution

Click through the tabs to see the steps of our solution.

Strategy

We’re going to use the \(x^n\)-method to help us calculate the limit. The reason for this is that as input \(x\) gets large positive, the numerator of the function is getting large positive and the denominator is getting large positive as well.

The result is what we call indeterminate form: \(\dfrac{\infty}{\infty}\)

Why the \(x^n\)-method works, is that it essentially converts terms that approach \(\infty\) with terms that approach \(0\). We can do arithmetic with actual numbers like \(0\), we cannot do usual arithmetic with \(\infty\).

Largest Power

We begin by identifying the largest power of \(x\) in the denominator, which in this case is \(x^2\). We then divide each term in both the numerator and denominator by \(x^2\). This is really accomplished by multiplying our function by a fancy \(1\):

\[ \dfrac{\tfrac{1}{x^2}}{\tfrac{1}{x^2}} \]

So let’s start with this in our limit calculation:

\[ \lim_{x\to \infty} \dfrac{3x^2-x-2}{5x^2+4x+1}\cdot \dfrac{\tfrac{1}{x^2}}{\tfrac{1}{x^2}} = \lim_{x\to \infty} \dfrac{3-\tfrac{1}{x}-\tfrac{2}{x^2}}{5+\tfrac{4}{x}+\tfrac{1}{x^2}} \]

Limit Laws

Most of our common limit laws still apply to these limits at infinity, so we next use the quotient limit law to get:

\[ \lim_{x\to \infty} \dfrac{3-\tfrac{1}{x}-\tfrac{2}{x^2}}{5+\tfrac{4}{x}+\tfrac{1}{x^2}} = \dfrac{\displaystyle \lim_{x\to \infty}\left(3-\tfrac{1}{x}-\tfrac{2}{x^2}\right)}{\displaystyle \lim_{x\to \infty}\left(5+\tfrac{4}{x}+\tfrac{1}{x^2}\right)} \]

After applying this quotient limit law, we just need to make sure that we do not end up with \(0\) in the denominator once we go through all of the calculations.

Next we can use the limit laws for sums, differences, and constant multiplication to get:

\[ =\dfrac{\displaystyle \lim_{x\to \infty}3-\lim_{x\to \infty}\tfrac{1}{x}-2\lim_{x\to \infty}\tfrac{1}{x^2}}{\displaystyle \lim_{x\to \infty} 5+4 \lim_{x\to \infty}\tfrac{1}{x}+\lim_{x\to \infty}\tfrac{1}{x^2}} \]

Basic Limits

At this point, each of these limits is one of our basic limits at infinity. Specifically:

\[ \lim_{x\to\infty}\dfrac{1}{x^n}=0 \quad \text{and}\quad \lim_{x\to\infty}k=k \]

Using this in our work we get:

\[\begin{split} & =\dfrac{\displaystyle \lim_{x\to \infty}3-\lim_{x\to \infty}\tfrac{1}{x}-2\lim_{x\to \infty}\tfrac{1}{x^2}}{\displaystyle \lim_{x\to \infty} 5+4 \lim_{x\to \infty}\tfrac{1}{x}+\lim_{x\to \infty}\tfrac{1}{x^2}} \\ & \\ & = \dfrac{3-0-2(0)}{5+4(0)+0} = \dfrac{3}{5} \end{split}\]

Notice that each of the limits in these last few steps ended up being an actual number - so we were able to do regular arithmetic with them.

Conclusion

Seeing how we calculated that:

\[ \lim_{x\to \infty} \dfrac{3x^2-x-2}{5x^2+4x+1} = \dfrac{3}{5} \]

we can additionally say that this function has a horizontal asymptote at \(y=3/5\). (Although this is not necessary to actually answer the original question.)

Strategy (\(x^n\)-method)

1. Identify the largest power of \(x\) in the denominator: \(x^n\).

2. Multiply both the numerator and denominator by \(\tfrac{1}{x^n}\)

Indeterminate Forms

We’ve just encountered our next major indeterminate form \(\tfrac{\infty}{\infty}\). And as we’re starting to suspect when we encounter them, more work is required to actually determine the limit. We cannot figure it out just from the expression \(\tfrac{\infty}{\infty}\) alone.

For indeterminate forms like this, the limit is a mystery until we do that additional work and it could ultimatley be:

• infinite: \(\infty\) or \(-\infty\)

• DNE: it might not exist

• some number \(L\)

Some of the indeterminate forms we will be seeing are listed below. What makes them indeterminate is that there is essentially a competition between two of the terms:

• one term wants to make the result really large.

• a second term wants to make the result really small.

And so the question is: Does the first term win, the second term win, or do they balance out in some way?

\[\begin{split} \textbf{Indeterminate Forms} & \qquad\dfrac{0}{0}\qquad \dfrac{\infty}{\infty} \qquad \infty - \infty \\ & \\ \textbf{Not Indeterminate}& \qquad\dfrac{c}{0}\qquad \dfrac{c}{\infty} \qquad \infty + \infty\\ \end{split}\]

---

Example 2

Compute the following limit:

\[ \lim_{x\to \infty} \dfrac{x^3+x^2}{4-x^2} \]

Solution

Click through the tabs to see the steps of our solution.

Strategy

We have another \(\tfrac{\infty}{\infty}\)-form here because as input \(x\) gets large positive, the numerator of the function is getting large positive and the denominator is getting large negative.

This means we should try using the \(x^n\)-method.

Largest Power

We begin by identifying the largest power of \(x\) in the denominator, which in this case is \(x^2\). Just like before, we then divide each term in both the numerator and denominator by \(x^2\) (which is really accomplished through multiplication by a fancy \(1\)).

\[ \dfrac{\tfrac{1}{x^2}}{\tfrac{1}{x^2}} \]

So let’s start with this in our limit calculation:

\[ \lim_{x\to \infty} \dfrac{x^3+x^2}{4-x^2}\cdot \dfrac{\tfrac{1}{x^2}}{\tfrac{1}{x^2}} = \lim_{x\to \infty} \dfrac{x+1}{\tfrac{4}{x^2}-1} \]

Limit Laws

We next want to try using our quotient limit law (since we are calculating the limit of a fraction).

Let’s look at the limits of our numerator and denominator separately:

• Numerator: \(\displaystyle \lim_{x\to\infty} (x+1)= \infty\)

• Denominator: \(\displaystyle \lim_{x\to\infty} \left(\tfrac{4}{x^2}-1\right)= -1\)

This means that for our fraction we have the numerator getting large positive while the denominator is getting closer to \(-1\). So essentially, we have:

\[ \dfrac{\text{large positive number}}{-1} \longrightarrow \text{large negative number} \]

Telling us that as input \(x\) gets large positive, the output of our function is getting large negative.

Conclusion

Since the output of our function is getting large negative, we conclude that the limit is given by:

\[ \lim_{x\to \infty} \dfrac{x^3+x^2}{4-x^2} = \lim_{x\to \infty} \dfrac{x+1}{\tfrac{4}{x^2}-1} = -\infty \]

Since this limit is infinite, we can also conclude that the function does not have a horizontal asymptote in the right-end direction.

Example 3

Compute the following limit:

\[ \lim_{x\to \infty} \left(x^3-x^2\right) \]

Solution

Click through the tabs to see the steps of our solution.

Identify

We first need to determine which type of form we have by looking at the individual parts of our function:

• First: \(\displaystyle \lim_{x\to\infty} x^3 =\infty\)

• Second: \(\displaystyle \lim_{x\to\infty} x^2 =\infty\)

Putting it all together gives us the indeterminate difference: \(\infty-\infty\). Our main strategy for these forms is to try and rewrite the function as a product.

Factor

We try factoring our function to get:

\[ \lim_{x\to \infty} \left(x^3-x^2\right) = \lim_{x\to \infty} x^2 \cdot\left(x-1\right) \]

Looking at each of these factors we see that:

• First: \(\displaystyle \lim_{x\to\infty} x^2 =\infty\)

• Second: \(\displaystyle \lim_{x\to\infty} (x-1) =\infty\)

Giving us a limit of the form \(\infty \cdot \infty\) which is not indeterminate. In fact if we have:

\[ \left(\text{large positive}\right)\cdot\left(\text{large positive}\right)\longrightarrow \text{large positive} \]

If we multiply two large positive numbers, it results in a larger positive number.

Conclusion

Since the output of our function is getting large positive, we conclude that the limit is given by:

\[ \lim_{x\to \infty} \left(x^3-x^2\right) = \lim_{x\to \infty} x^2 \cdot\left(x-1\right) = \infty \]

Since this limit is infinite, we can also conclude that the function does not have a horizontal asymptote in the right-end direction.

Strategy (Factor)

One strategy for the indeterminate form \({\infty-\infty}\) is to:

• rewrite the expression as a product (factor)

Example 4

Compute the following limit:

\[ \lim_{x\to -\infty} \left(\sqrt{x^2+25}+x\right) \]

Solution

Click through the tabs to see the steps of our solution.

Identify

We first need to determine which type of form we have by looking at the individual parts of our function:

• First: \(\displaystyle \lim_{x\to-\infty} \sqrt{x^2+25} =\infty\)

• Second: \(\displaystyle \lim_{x\to-\infty} x =-\infty\)

Putting it all together gives us the indeterminate difference: \(\infty-\infty\). Usually, we try factoring when we have these types of forms. However, another strategy that can be helpful, especially when we see a square root function, is to multiply by a fancy \(1\). Specifically,

\[ \dfrac{\text{conjugate}}{\text{conjugate}} \]

Conjugate

We start our calculations by multiplying by the necessary conjugate terms:

\[ \lim_{x\to -\infty} \left(\sqrt{x^2+25}+x\right)\cdot \dfrac{\sqrt{x^2+25}-x}{\sqrt{x^2+25}-x} \]

Multiplying out the numerators gives us:

\[ =\lim_{x\to -\infty} \dfrac{x^2+25-x^2}{\sqrt{x^2+25}-x} \]

And canceling the \(x^2\) terms, we get:

\[ =\lim_{x\to -\infty} \dfrac{25}{\sqrt{x^2+25}-x} \]

Denominator

Let’s consider what is now happening with the term in the denominator:

\[ \lim_{x\to -\infty} \left(\sqrt{x^2+25}-x\right) \]

• First: \(\displaystyle \lim_{x\to-\infty} \sqrt{x^2+25} =\infty\)

• Second: \(\displaystyle \lim_{x\to-\infty} -x =\infty\)

So we actually have a \(\infty +\infty\) form here, which is not indeterminate - we know what this is doing:

\[ \text{large positive} + \text{large positive} \longrightarrow \text{large positive} \]

Therefore, the limit of just the denominator term is infinite:

\[ \lim_{x\to -\infty} \left(\sqrt{x^2+25}-x\right) =\infty \]

Conclusion

Since the limit of just the denominator is infinite that means the entire limit:

\[ \lim_{x\to -\infty} \dfrac{25}{\sqrt{x^2+25}-x} \]

is a \(\tfrac{c}{\infty}\)-form, which we know go to \(0\). Therefore we can conclude:

\[ \lim_{x\to -\infty} \left(\sqrt{x^2+25}+x\right) = \lim_{x\to -\infty} \dfrac{25}{\sqrt{x^2+25}-x} =0 \]

Strategy (Conjugate)

A strategy for intedeterminate forms involving the sum of a square root term is to use the conjugate and:

• multiply by \(\dfrac{\text{conjugate}}{\text{conjugate}}\)

Example 5

Find all horizontal asymptotes of the given function.

\[ f(x)=\dfrac{\sqrt{4x^2+1}}{3x-5} \]

Solution

Click through the tabs to see the steps of our solution.

Strategy

In order to find all horizontal asymptotes, we need to calculate both limits at infinity. We could have one asymptote in the right-end direction and then a completely different asymptote in the left-end direction.

This means we need to calculate both the right-end limit:

\[ \lim_{x\to\infty} \dfrac{\sqrt{4x^2+1}}{3x-5} \]

And the left-end limit:

\[ \lim_{x\to-\infty} \dfrac{\sqrt{4x^2+1}}{3x-5} \]

Right End

We are going to start with the right-end limit. Since this is an \(\tfrac{\infty}{\infty}\)-form, we are going to try using our \(x^n\)-method. The largest power of \(x\) in the denominator is \(x\), so we will multiply both the numerator and denominator by \(\tfrac{1}{x}\).

\[ \lim_{x\to\infty} \dfrac{\sqrt{4x^2+1}}{3x-5}\cdot\dfrac{\tfrac{1}{x}}{\tfrac{1}{x}} \]

In order to simplify the numerator we need to make the terms there match (make both have a square root function). How can we rewrite \(\tfrac{1}{x}\) so that it has a square root?

Since \(x\to \infty\), that means \(x\) is ultimately positive. By our helpful properties listed below, we see that for positive \(x\) a rewrite is possible: \(x=\sqrt{x^2}\). Using this just in the numerator, gives us:

\[ = \lim_{x\to\infty} \dfrac{\sqrt{4x^2+1}}{3x-5}\cdot\dfrac{\tfrac{1}{\sqrt{x^2}}}{\tfrac{1}{x}} \]

By the other helpful property, we can bring both of those square root terms under one big square root sign:

\[ = \lim_{x\to\infty} \dfrac{\sqrt{\left(4x^2+1\right)\cdot \tfrac{1}{x^2} }}{\left(3x-5\right)\cdot \tfrac{1}{x}} \]

Helpful Properties

\[\begin{split} \dfrac{\sqrt{a}}{\sqrt{b}} & = \sqrt{\dfrac{a}{b}} \\ & \\ \sqrt{u^2} & = \begin{cases} u & \quad \text{if} \quad u \geq 0 \\ -u & \quad \text{if} \quad u <0 \\ \end{cases} \\ \end{split}\]

Limit Laws

Now we can simplify we get:

\[ \lim_{x\to\infty} \dfrac{\sqrt{\left(4x^2+1\right)\cdot \tfrac{1}{x^2} }}{\left(3x-5\right)\cdot \tfrac{1}{x}} = \lim_{x\to\infty} \dfrac{\sqrt{4+\tfrac{1}{x^2} }}{3-\tfrac{5}{x}} \]

And then using our limit laws we can split up the limit sign over the quotient and bring the limit inside the square root:

\[ = \dfrac{\displaystyle \sqrt{\lim_{x\to\infty} \left(4+\tfrac{1}{x^2}\right) }}{\displaystyle \lim_{x\to\infty}\left(3-\tfrac{5}{x}\right)} \]

And from here we have basic limits at infinity, so we get:

\[ =\dfrac{\sqrt{4+0}}{3-0} = \dfrac{2}{3} \]

Conclusion

We just finished showing that the right-end limit is:

\[ \lim_{x\to\infty} \dfrac{\sqrt{4x^2+1}}{3x-5} = \dfrac{2}{3} \]

This means that the function has a horizontal asymptote at \(y=\tfrac{2}{3}\).

---

Similar calculations can be performed to show that the left-end limit is:

\[ \lim_{x\to-\infty} \dfrac{\sqrt{4x^2+1}}{3x-5} = -\dfrac{2}{3} \]

Which means that the function also has a horizontal asymptote at \(y=-\tfrac{2}{3}\).

---

Note: As practice, you should try calculating the left-end limit yourself, using the above steps as a guide. The one tricky step that will take a little care, is when you convert the term \(\tfrac{1}{x}\) into a term with a square root.

For the left-end limit, \(x\to -\infty\), which means that \(x\) is ultimately negative. From our helpful properties listed before, we see that for \(x\) negative: \(-x=\sqrt{x^2}\) or alternatively, \(x=-\sqrt{x^2}\). Therefore, we would have:

\[ \lim_{x\to-\infty} \dfrac{\sqrt{4x^2+1}}{3x-5} = \lim_{x\to-\infty} \dfrac{\sqrt{4x^2+1}}{3x-5}\cdot\dfrac{\tfrac{1}{x}}{\tfrac{1}{x}} = \lim_{x\to-\infty} \dfrac{\sqrt{4x^2+1}}{3x-5}\cdot\dfrac{\tfrac{-1}{\sqrt{x^2}}}{\tfrac{1}{x}} \]

The rest of the work would be very similar to what we did before, only that there is an extra negative to keep track of this time.

Converting Limits to Limits at Infinity

Sometimes we might be presented with a limit involving a composite function. If the limit of the inner function is infinite (becomes very large positive or negative), we may need to use a change of variables to help actually calculate the limit.

Change of Variables

1. Let \(u=\) inner function (change of variables)

2. Compute \(\displaystyle \lim_{x\to a} u\)

3. Compute the limit of the function with the changed variables.

Example 6

Compute the following limit:

\[ \lim_{x\to 0^-} e^{1/x} \]

Solution

Click through the tabs to see the steps of our solution.

Identify

We begin by noticing that this is composite function with inner function \(\tfrac{1}{x}\).

The issue here is that the limit of the inner function is infinite as \(x\to 0^-\). And we cannot plug \(\infty\) into the exponential function since it is not a number. To deal with this, we are going to use a change of variables and introduce new variable \(u\):

\[ u=\dfrac{1}{x} \qquad\text{(the inner function)} \]

Inner Limit

We next calculate the limit of this inner function:

\[ \lim_{x\to0^-} u = \lim_{x\to0^-} \dfrac{1}{x} \]

We calculate this limit by first noting that we have a \(\tfrac{c}{0}\)-form which means either it is \(\infty\) or \(-\infty\). Next we use a test number to decide on positive or negative. Since \(x\) is approaching \(0\) from the left, we need to use a test number that is close to \(0\), but slightly smaller, so \(t=-0.1\) would work. Plugging this into \(\tfrac{1}{x}\) gives us negative number \(\tfrac{1}{-0.1}\). Allowing us to say:

\[ \lim_{x\to0^-} u = \lim_{x\to0^-} \dfrac{1}{x}=-\infty \]

Essentially what this tells us is that as \(x\to 0^-\), the expression \(u\to -\infty\).

Convert

With all of the pieces ready, we compute the original limit by changing all \(x\)-terms into this new variable:

\[ \lim_{x\to 0^-} e^{1/x} = \lim_{u\to -\infty} e^{u} \]

Where we changed:

• the \(\tfrac{1}{x}\) in the exponent to \(u\) and

• the limit from \(\displaystyle \lim_{x\to 0^-} \) to \(\displaystyle \lim_{u\to -\infty} \)

Conclusion

But now, this limit is one of our basic limits at infinity which we know:

\[ \lim_{x\to 0^-} e^{1/x} = \lim_{u\to -\infty} e^{u} = 0 \]

And there we have it!

Example 7

Compute the following limit:

\[ \lim_{x\to 2^+} \tan^{-1}\left(\dfrac{1}{x-2}\right) \]

Solution

Click through the tabs to see the steps of our solution.

Identify

We begin by noticing that this is composite function with inner function \(\tfrac{1}{x-2}\).

The issue here is that the limit of the inner function is infinite as \(x\to 2^+\). And we cannot plug \(\infty\) into the inverse tangent function since it is not a number. To deal with this, we are going to use a change of variables and introduce new variable \(u\):

\[ u=\dfrac{1}{x-2} \qquad\text{(the inner function)} \]

Inner Limit

We next calculate the limit of this inner function:

\[ \lim_{x\to2^+} u = \lim_{x\to2^+} \dfrac{1}{x-2} \]

We calculate this limit by first noting that we have a \(\tfrac{c}{0}\)-form which means either it is \(\infty\) or \(-\infty\). Next we use a test number to decide on positive or negative. Since \(x\) is approaching \(2\) from the right, we need to use a test number that is close to \(2\), but slightly larger, so \(t=2.1\) would work. Plugging this into \(\tfrac{1}{x-2}\) gives us positive number \(\tfrac{1}{0.1}\). Allowing us to say:

\[ \lim_{x\to2^+} u = \lim_{x\to2^+} \dfrac{1}{x-2}=\infty \]

Essentially what this tells us is that as \(x\to2^+\), the expression \(u\to \infty\).

Convert

With all of the pieces ready, we compute the original limit by changing all \(x\)-terms into this new variable:

\[ \lim_{x\to 2^+} \tan^{-1}\left(\dfrac{1}{x-2}\right) = \lim_{u\to \infty} \tan^{-1}({u}) \]

Where we changed:

• the \(\tfrac{1}{x-2}\) in the exponent to \(u\) and

• the limit from \(\displaystyle \lim_{x\to 2^+} \) to \(\displaystyle \lim_{u\to \infty} \)

Conclusion

The resulting limit is one of our basic limits at infinity which we know:

\[ \lim_{x\to 2^+} \tan^{-1}\left(\dfrac{1}{x-2}\right) = \lim_{u\to \infty} \tan^{-1}({u}) = \dfrac{\pi}{2} \]

Done!