(L4) Infinite Limits

By the end of the lesson you will be able to:

• find the infinite limits of a function using graphical, numerical, and algebraic means.

• use infinite limits to find any vertical asymptotes in the graph of a function.

Lecture Video

---

Introduction

Graphical

Consider the graph of the following function:

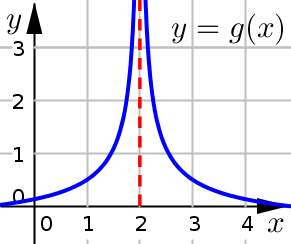
In this graph, we see that as \(x\) moves towards \(a\) (from either side) the height of our curve gets very large positive.

To denote this we say:

\[ \lim_{x\to a} g(x)=\infty \]

---

Numerical

Consider the following table of function values:

\(x\)	\(f(x)\)
\(0.9\)	\(-10\)
\(0.99\)	\(-100\)
\(0.999\)	\(-1000\)
\(0.9999\)	\(-10000\)
\(0.99999\)	\(-100000\)

In this table, we can see that as the input values \(x\) get closer to the number \(1\) from the left, the output values of our function get very large negative.

To denote this we say:

\[ \lim_{x\to 1^-} f(x)=-\infty \]

---

Definition of Infinite Limits

Positive Infinity

\[ \lim_{x\to a} f(x)=\infty \]

As input values, \(x\), get close to value \(a\), the output values, \(f(x)\), get very large positive.

Negative Infinity

\[ \lim_{x\to a} f(x)=-\infty \]

As input values, \(x\), get close to value \(a\), the output values, \(f(x)\), get very large negative.

Notes

1. The symbol \(\infty\) is not a number. This means that we cannot do (normal) arithmetic with it.

2. Technically, the limit in each of these definitions does not exist, but we use these infinity symbols, \(\infty\) and \(-\infty\), to better describe the specific way the limit does not exist.

---

Locating an Infinite Limit

General Strategy

Infinite limits usually occur when we have division, and in particular, when we attempt to divide a non-zero number by \(0\) we call this the:

\[ \dfrac{c}{0}\text{ -form} \]

Strategy for Division

1. Identify that the limit is a \(\tfrac{c}{0}\)-form (plug-in).

2. Recognize that this means the limit is either \(+\infty\) or \(-\infty\).

3. Use a test number to determine which it is.

Special Case

Like we said above, in most of the functions we will be looking at, infinite limits occur when there is division involved. However there is one special case that shows up frequently:

\[ \lim_{x\to 0^+} \ln x = -\infty \]

---

Vertical Asymptotes

Vertical Asymptote

The vertical line \(x=a\) is called a vertical asymptote of the curve \(y=f(x)\) provided there is an infinite limit on the left, right, or both sides of \(a\).

If we consider the same graph from earlier:

We see that this function has a vertical asymptote at the line \(x=2\), since there is at least one infinite limit there. In actuality, there are two infinite limits for this graph, one on either side.)

Graphically, a vertical asymptote is the vertical line the graph of our function is getting closer and closer to.

Locating Vertical Asymptotes

Since vertical asymptotes occur where we have a infinite limit, we usually have a vertical asymptotes at \(x\)-values where we attempt to divide a non-zero number by \(0\). So the way we locate a vertical asymptote is exactly the same procedure that we would use to locate the places where our function has an infinite limit.

Locating a Vertical Asymptote

1. Find where denominator \(=0\).

2. Show that there is an infinite limit on the left, right, or both sides of this location.

Special Case

As before, the natural logarithmic function is a special case and has a vertical asymptote at \(x=0\) since the right side limit is infinite:

\[ \lim_{x\to 0^+} \ln x = -\infty \]

Example 1

Compute the following limits:

(a) \(\displaystyle \lim_{x\to 4^-} \dfrac{1+x}{4-x}\)

Step 1: Identify that this is a \(\tfrac{c}{0}\)-form by plugging in \(x=4\)

\[ x=4 \longrightarrow \dfrac{1+4}{4-4}=\dfrac{5}{0} \]

Step 2: Seeing this, tells us that the limit is either going to be \(+\infty\) or \(-\infty\).

Setp 3: Use a test number to determine the sign of our function near \(x=4\) on the left. We want to pick a test number that is close to \(4\) but slightly smaller. There are a lot of options but \(t=3.9\) will work. Plug this into the function and see what you get:

\[ t=3.9 \longrightarrow \dfrac{1+3.9}{4-3.9}= \dfrac{4.9}{0.1} \]

Because this result is positive, we can conclude that the limit is positive infinity:

\[ \lim_{x\to 4^-} \dfrac{1+x}{4-x} =+\infty \]

(b) \(\displaystyle \lim_{x\to 4^+} \dfrac{1+x}{4-x}\)

Step 1: Identify that this is a \(\tfrac{c}{0}\)-form by plugging in \(x=4\) (same as before)

\[ x=4 \longrightarrow \dfrac{1+4}{4-4}=\dfrac{5}{0} \]

Step 2: Seeing this, tells us that the limit is either going to be \(+\infty\) or \(-\infty\).

Setp 3: Use a test number to determine the sign of our function near \(x=4\) on the right. We want to pick a test number that is close to \(4\) but slightly larger, since we are on the right. Using \(t=4.1\) will work. Plug this into the function and see what you get:

\[ t=4.1 \longrightarrow \dfrac{1+4.1}{4-4.1}= \dfrac{5.1}{-0.1} \]

Because this result is negative, we can conclude that the limit is negative infinity:

\[ \lim_{x\to 4^+} \dfrac{1+x}{4-x} =-\infty \]

(c) \(\displaystyle \lim_{x\to 4} \dfrac{1+x}{4-x}\)

Since the left and right sided limits are behaving differently, we say the overall limit does not exist. That is,

\[ \lim_{x\to 4} \dfrac{1+x}{4-x} \quad \text{DNE} \]

Example 2

Show that the following function has a vertical asymptote at the indicated \(x\)-value:

\[f(x)=\tan x\qquad\text{at}\quad x=\dfrac{\pi}{2}\]

Solution

Click through the tabs to see the steps of our solution.

Quotient

In order to show that we have a vertical asymptote, it is enough to show that either the left or right limit is infinite. (We will show both in this case, just for the practice.)

However, before we get started with the left limit, the first thing we might notice is that this function is not a quotient. Well, we can actually rewrite \(\tan x\) as a fraction:

\[ \tan x = \dfrac{\sin x}{\cos x} \]

Left Limit

We start by calculating the left-sided limit:

\[ \lim_{x\to \pi/2^-} \dfrac{\sin x}{\cos x} \]

Step 1: Identify that this is a \(\tfrac{c}{0}\)-form by plugging in \(x=\pi/2\)

\[ x=\pi/2 \longrightarrow \dfrac{\sin \left(\pi/2\right)}{\cos \left(\pi/2\right)} = \dfrac{1}{0} \]

Step 2: Seeing this, tells us that the limit is either going to be \(+\infty\) or \(-\infty\).

Setp 3: Use a test number to determine the sign of our function near \(x=\pi/2\) on the left.

• If we consult the graph of \(\sin x\), we see that near \(\pi/2\) on the left, the sine function is positive.

• The graph of \(\cos x\), shows us that near \(\pi/2\) on the left, the cosine function is positive.

Putting this together, tells us that near \(\pi/2\) on the left, the tangent function must be positive. So we conclude:

\[ \lim_{x\to \pi/2^-} \dfrac{\sin x}{\cos x} = +\infty \]

Showing this limit to be infinite, is actually enough work to show that we have a vertical asymptote at \(x=\pi/2\).

Right Limit

For practice though, let’s also calculate the right-sided limit:

\[ \lim_{x\to \pi/2^+} \dfrac{\sin x}{\cos x} \]

Step 1: Identify that this is a \(\tfrac{c}{0}\)-form by plugging in \(x=\pi/2\)

\[ x=\pi/2 \longrightarrow \dfrac{\sin \left(\pi/2\right)}{\cos \left(\pi/2\right)} = \dfrac{1}{0} \]

Step 2: This tells us that the limit is either going to be \(+\infty\) or \(-\infty\).

Setp 3: Use a test number to determine the sign of our function near \(x=\pi/2\) on the right.

• If we consult the graph of \(\sin x\), we see that near \(\pi/2\) on the right, the sine function is positive.

• The graph of \(\cos x\), shows us that near \(\pi/2\) on the right, the cosine function is negative.

Putting this together, tells us that near \(\pi/2\) on the right, the tangent function must be negative. So we conclude:

\[ \lim_{x\to \pi/2^+} \dfrac{\sin x}{\cos x} = -\infty \]

Overall Limit

Although this is not necessary to answer the question, it is helpful to note that since the left and right sided limits are behaving differently, we would say the overall limit does not exist. That is,

\[ \lim_{x\to \pi/2} \dfrac{\sin x}{\cos x} \quad \text{DNE} \]