(IC3) Net Change#

By the end of the lesson you will be able to:

  • Use definite integrals to calculate the displacement of an object moving in a straight line.

  • Use definite integrals to calculate the total distance traveled by an object moving in a straight line.

  • Use definite integrals to calculate the net change.

Lecture Videos#

Net Change#

Net Change Theorem

\[ \int_a^b F'(x)\; dx = F(b)-F(a) \]

The equation described by the Net Change Theorem, looks similar to what we have seen with the Fundamental Theorem of Calculus (part 2) with the specific case here of integrating a derivative \(F'\).

\[ \int_a^b F'(x)\; dx = F(b)-F(a) \]

What we’re going to investigate is how to interpret this equation.

\[ \underbrace{\int_a^b F'(x)\; dx}_{ \text{Definite integral of } F' \text{over }[a,b]} = F(b)-F(a) \]

This definite integral represents the cumulative effect on \(F\) of all those instantaneous little changes described by \(F'\) over the interval \([a,b]\).

Essentially (if we’re thinking time), the quantity described by \(F\) experiences instantaneous changes described by \(F'\) at each moment of time in the interval \([a,b]\).

What we’re doing with the definite integral then is somehow adding up all of these tiny little changes to see the big picture: how \(F\) changes over the entire interval.

\[ \int_a^b F'(x)\; dx = \underbrace{F(b)-F(a)}_{ \text{net change of } F \text{ over }[a,b]} \]

What we’re seeing on the right side of this equation is the net change of \(F\) over the interval \([a,b]\). The net change is the difference of the ending and starting values:

  • \(F(a)\) is the starting value

  • \(F(b)\) is the ending value

\[ \underbrace{\int_a^b F'(x)\; dx}_{\text{sum of all instantaneous changes}} = \underbrace{F(b)-F(a)}_{\text{net change}} \]

Putting this all together, we see that the net change theorem is telling us:

  • if we add up all of those little instantaneous changes described by \(F'\) (the integration),

  • what we get is a numerical value describing how much \(F\) changed over that entire interval.

Volume of a Reservoir#

Let \(V(t)\) be the volume of water in a reservoir at time \(t\). This reservoir is set up so that water is allowed to flow in and flow out.

Since \(V\) represents the volume, the first derivative \(V'(t)\) represents the rate at which this volume is changing at time \(t\). And its helpful to keep in mind that:

  • If \(V'\) is positive, then volume \(V\) is increasing.

  • If \(V'\) is negative, then volume \(V\) is decreasing.

(This is the usual increasing / decreasing relationship that we saw in the optimization lessons.)

What would integrating the derivative give us in this case?

\[ \underbrace{\int_a^b V'(t) \; dt}_{\text{definite integral}} = V(b)-V(a) \]

Remember that \(V'(t)\) describes the rate at which the volume is changing at time \(t\). Essentially what we’re doing then with this definite integral is:

  • taking all of these small instantaneous changes in the volume

  • and adding them together in some way.

What the net change theorem says in this case, is that if we add up all of the instantaneous volume changes, what we get is the net change in the volume.

This is what we see on the right side of the equation:

\[ \int_a^b V'(t) \; dt = \underbrace{V(b)-V(a)}_{\text{net change}} \]

  • \(V(a)\) is the starting volume of water

  • \(V(b)\) is the ending volume of water

So the net change in volume is just the ending volume measurement minus the starting volume measurement.

The definite integral can then be interpreted as the net change in the water level: ending volume minus starting volume:

  • If the definite integral is positive, then there was a net increase in volume during that time interval.

  • If the definite integral is negative, then there was a net decrease in volume during that time interval.

  • If the definite integral is zero, then there was a net change of zero during this time interval. This is not to say that no water flowed in or out, but rather to say that the amount of water that did flow in was equal to the amount of water that flowed out.

As an example, suppose we had the following as our graph of \(V'\) over some time interval \([a,b]\).

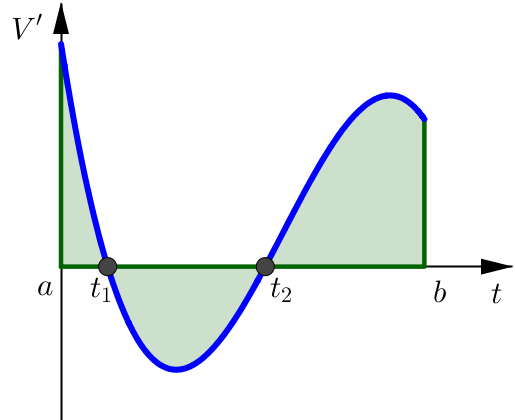
Derivative of a volume function

We can then relate the geometric area under the curve to the changes in volume. We can see 3 distinct regions for this \(V'\) curve:

First Region over the interval \([a,t_1]\). Since the function \(V'\) is above the horizontal axis in this region, the definite integral would then be positive and represent:

\[ \int_{a}^{t_1} V'(t)\; dt \longrightarrow \left( \text{Area} \atop \text{Above} \right) \quad \text{or}\quad \left( \text{Volume of} \atop \text{water increase} \right) \]

Second Region over the interval \([t_1,t_2]\). Since the function \(V'\) is below the horizontal axis in this region, the definite integral would then be negative and represent:

\[ \int_{t_1}^{t_2} V'(t)\; dt \longrightarrow -\left( \text{Area} \atop \text{Below} \right) \quad \text{or}\quad -\left( \text{Volume of} \atop \text{water decrease} \right) \]

Third Region over the interval \([t_2,b]\). Since the function \(V'\) is above the horizontal axis in this region, the definite integral would then be positive and represent:

\[ \int_{t_2}^{b} V'(t)\; dt \longrightarrow \left( \text{Area} \atop \text{Above} \right) \quad \text{or}\quad \left( \text{Volume of} \atop \text{water increase} \right) \]

All Together

Putting this all together then, we see that the entire definite integral from \(a\) to \(b\) can be thought of a few ways: in the context of our volume function, or just geometrically as area under the curve.

\[ \int_{a}^{b} V'(t)\; dt = \int_{a}^{t_1} V'(t)\; dt\; + \; \int_{t_1}^{t_2} V'(t)\; dt \; + \; \int_{t_2}^{b} V'(t)\; dt \]

Volume

\[ \left( \text{Net Change in } \atop \text{volume over }[a,b] \right) = \left( \text{Volume of water } \atop \text{increase during }[a,t_1] \right) \; - \; \left( \text{Volume of water } \atop \text{decrease during }[t_1,t_2] \right)\; + \; \left( \text{Volume of water } \atop \text{increase during }[t_2,b] \right) \]

Area under Curve

\[ \left( \text{Net area } \atop \text{over }[a,b] \right) = \left( \text{Area Above} \atop \text{over }[a,t_1] \right) \; - \; \left( \text{Area Below} \atop \text{over }[t_1,t_2] \right)\; + \; \left( \text{Area Above} \atop \text{over }[t_2,b] \right) \]

Motion in a Straight Line#

Let’s consider the case where an object is moving in a straight line. In this specific case the Net Change Theorem would be:

\[ \int_a^b v(t)\; dt = \int_a^b s'(t)\; dt = s(b)-s(a) \]

In this result, we see a few different functions to remember:

  • Position function denoted by \(s(t)\) and represents the location of the object at time \(t\).

  • Velocity function denoted by \(v(t)=s'(t)\). If we think of this function as the derivative of the position function, it describes the instantaneous rate of change in position at each moment of time during interval \([a,b]\).

Remember that there is a direction component to both of these functions. If velocity is negative, that means the object is moving in the negative direction and if velocity is positive, the object is moving in the positive direction.

  • Negative direction is usually either down or left.

  • Positive direction is usually either up or right.

What the net change theorem is then telling us is that by integrating \(s'(t)\) over the interval \([a,b]\) we are essentially adding up all of those instantaneous little changes in our position and producing the big picture: how much are position changed over that entire interval \([a,b]\)

\[ \int_a^b v(t)\; dt = \int_a^b s'(t)\; dt = s(b)-s(a) \]

Remember that we call the quantity \(s(b)-s(a)\) the displacement.

  • \(s(a)\) is the starting position

  • \(s(b)\) is the ending position

So the net change in position is just the ending position measurement minus the starting position measurement.

The definite integral can then be interpreted as the net change in position: ending location minus starting location:

  • If the definite integral is positive, then relative to the starting location, the ending location of the object is in the positive direction.

  • If the definite integral is negative, then relative to the starting location, the ending location of the object is in the negative direction.

  • If the definite integral is zero, then the starting and ending locations are exactly the same. This is not to say that the object necessarily stayed motionless the entire time, but rather to say that it may have moved and bounced around, but it started and stopped at the exact same location.

Displacement measures the distance and direction between the starting position and the ending position of the object.

If we know the velocity function we can calculate it by:

\[\begin{split} \begin{aligned} \left( \text{Displacement } \atop \text{over }[a,b] \right) & = \int_a^b v(t)\; dt \\ & \\ & = \left( \text{Distance in} \atop + \text{ direction} \right) - \left( \text{Distance in} \atop - \text{ direction} \right)\\ \end{aligned} \end{split}\]

Note that displacement can be positive, zero, or negative.

Total Distance measures the length of the path traced out by the moving object during a given time interval. Total distance can only be positive (or zero if the object isn’t moving at all).

If we know the velocity function we can calculate total distance by:

\[\begin{split} \begin{aligned} \left( \text{Total Distance } \atop \text{over }[a,b] \right) & = \int_a^b \big| v(t) \big| \; dt \\ & \\ & = \left( \text{Distance in} \atop + \text{ direction} \right) + \left( \text{Distance in} \atop - \text{ direction} \right)\\ \end{aligned} \end{split}\]

Since this total distance formula involves an absolute value sign inside the integral, the only way to calculate this definite integral is to:

  1. Determine where \(v(t)\) is positive / negative using a sign chart.

  2. Integrate over each of these subintervals separately.

  3. Add the results.

Example 1#

A rocket is fired vertically into the air. Its velocity at \(t\) seconds after liftoff is \(v(t)=-32t+160\) feet per second. Consider the time interval \(0\leq t \leq 8\).

  1. Find the displacement of the rocket during this time interval.

  2. Find the total distance traveled by the rocket during this time interval.

Click through the tabs to see the solution.

Give this a try for yourself first!

There are a few ways to calculate the displcament for a moving object:

  • If we know the position function \(s(t)\), we could calculate \(s(b)-s(a)\).

  • But since we only know velocity function \(v(t)\), we instead calculate:

\[\begin{split} \begin{aligned} \left(\text{Displacement} \atop \text{over } [0,8] \right) & = \int_0^8 v(t) \; dt \\ & \\ & = \int_0^8 \big(-32t+160 \big) \; dt \\ & \\ & = \big(-16t^2+160t \big) \bigg|_{t=0}^{t=8} \\ & \\ & = \big(-16(8^2)+160(8) \big) - \big(-16(0^2)+160(0) \big)\\ & \\ & = 256 \; \text{ft}\\ \end{aligned} \end{split}\]

In order to determine the total distance, we need to separately determine the distance it travels in the positive direction and the distance it travels in the negative direction. And in order to do this, we need to determine when it’s moving in these directions. We do this with a sign chart:

Intersection Points

The only way the velocity can switch signs between \(+\) and \(-\), is if there is a point in the middle where it is \(=0\). These are the \(t\)-intercepts, where the velocity function intersects the horizontal axis.

We start by setting \(v(t)=0\) and solving for \(t\).

\[\begin{split} v(t) = 0 & \xrightarrow{\text{set up}} -32t+160=0 \\ & \\ & \xrightarrow{\text{move terms}} 160=32t \\ & \\ & \xrightarrow{\text{divide} } t= \dfrac{160}{32} = 5 \\ \end{split}\]

Sign Chart

This \(t\)-value we just found, \(t=5\), splits up the interval \([0,8]\) into separate subintervals: \([0,5)\) and \((5,8]\).

We use these intervals to help create the sign chart for \(v\). Since there aren’t many factors for this function, we could just use immediately use test numbers to help determine the sign:

\[\begin{split} \begin{aligned} & t=1 \xrightarrow{\text{test number for } [0,5)} v(1)=-32(1)+160=+128 \\ & \\ & t=6 \xrightarrow{\text{test number for } (5,8]} v(6)=-32(6)+160=-32 \\ \end{aligned} \end{split}\]
\[\begin{split} \begin{array}{ccc} & [0,5)& (5,8] \\ \hline v & + & - \\ \hline \text{Direction} & + \text{ Direction} & - \text{ Direction} \\ \hline \end{array} \end{split}\]

To calculate the distance traveled by the rocket in the positive direction, we are going to calculate the definite integral of \(v(t)\) over the interval \([0,5)\). (This is the time interval where it is moving in the positive direction found in the sign chart.)

Since \(v(5)=0\), we can extend this interval to \([0,5]\) without changing the value we get for distance.

\[\begin{split} \begin{aligned} \left(\text{Distance in} \atop + \text{ Direction} \right) & = \int_0^5 v(t) \; dt \\ & \\ & = \int_0^5 \big(-32t+160 \big) \; dt \\ & \\ & = \big(-16t^2+160t \big) \bigg|_{t=0}^{t=5} \\ & \\ & = \big(-16(5^2)+160(5) \big) - \big(-16(0^2)+160(0) \big)\\ & \\ & = 400 \; \text{ft}\\ \end{aligned} \end{split}\]

To calculate the distance traveled by the rocket in the negative direction, we are going to calculate the definite integral of \(v(t)\) over the interval \((5,8]\). (This is the time interval where it is moving in the negative direction found in the sign chart.)

Since \(v(5)=0\), we can extend this interval to \([5,8]\) without changing the value we get for distance.

\[\begin{split} \begin{aligned} \int_5^8 v(t) \; dt & = \int_5^8 \big(-32t+160 \big) \; dt \\ & \\ & = \big(-16t^2+160t \big) \bigg|_{t=5}^{t=8} \\ & \\ & = \big(-16(8^2)+160(8) \big) - \big(-16(5^2)+160(5) \big)\\ & \\ & = -144 \\ \end{aligned} \end{split}\]

Why is this integral negative? Because on this interval \((5,8]\), the velocity function is entirely negative. So what this value is telling us is that during this time interval, the rocket moved \(144 \text{ ft}\) in the negative direction.

However, with total distance we want to know how much we traveled not so much the direction we traveled in. So we make an adjustment by instead using the negative of the integral:

\[\begin{split} \begin{aligned} \left(\text{Distance in} \atop - \text{ Direction} \right) & = -\int_5^8 v(t) \; dt \\ & \\ & = -(-144) \; \text{ft} & \\ & = 144 \; \text{ft} \end{aligned} \end{split}\]

Now that we have the distance traveled in the positive direction and the distance traveled in the negative direction, we can put these together to get the total distance.

\[\begin{split} \begin{aligned} \text{Total Distance} & = \left(\text{Distance in} \atop + \text{ Direction} \right) + \left(\text{Distance in} \atop - \text{ Direction} \right) \\ & \\ & = 400 \; \text{ft} + 144 \; \text{ft}\\ & \\ & = 544 \; \text{ft}\\ \end{aligned} \end{split}\]

Although, not normally how we do it, we can calculate the displacement using the distance traveled in the positive direction and the distance traveled in the negative direction.

\[\begin{split} \begin{aligned} \text{Displacement} & = \left(\text{Distance in} \atop + \text{ Direction} \right) -\left(\text{Distance in} \atop - \text{ Direction} \right) \\ & \\ & = 400 \; \text{ft} - 144 \; \text{ft} \\ & \\ & = 256 \; \text{ft} \\ \end{aligned} \end{split}\]

Which we see agrees with our previous result for displacement.

It is helpful to note that the calculations we have just done for displacement and total distance are very similar to the calculations we do with net area and total area. In fact, if we graph the velocity function:

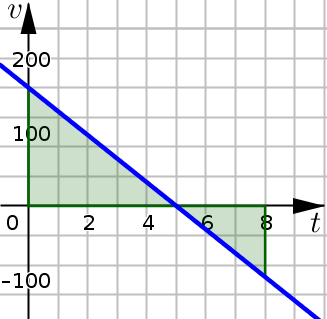
Graph of a piecewise function

and approach this problem as finding net area and total area we would see that:

\[\begin{split} \begin{aligned} & \left(\text{Area Above} \atop \text{over } [0,5]\right) \xrightarrow{\text{corresponds with}} \left(\text{Distance in} \atop + \text{ Direction} \right) \\ & \\ & \left(\text{Area Below} \atop \text{over } [5,8]\right) \xrightarrow{\text{corresponds with}} \left(\text{Distance in} \atop - \text{ Direction} \right) \\ \end{aligned} \end{split}\]

Example 2#

A particle moves along a line so that its velocity at time \(t\) is given by:

\[ v(t) = t^2-t-6 \]

measured in \(\text{m/s}\). Consider the time interval \(1\leq t\leq 4\).

  1. Find the displacement of the particle during this time interval.

  2. Find the total distance traveled by the particle during this time interval.

Click through the tabs to see the solution.

Give this a try for yourself first!

There are a few ways to calculate the displcament for a moving object:

  • If we know the position function \(s(t)\), we could calculate \(s(b)-s(a)\).

  • But since we only know velocity function \(v(t)\), we instead calculate:

\[\begin{split} \begin{aligned} \left(\text{Displacement} \atop \text{over } [1,4] \right) & = \int_1^4 v(t) \; dt \\ & \\ & = \int_1^4 \big(t^2-t-6 \big) \; dt \\ & \\ & = \big(\tfrac{1}{3}t^3-\tfrac{1}{2}t^2-6t \big) \bigg|_{t=1}^{t=4} \\ & \\ & = \big(\tfrac{1}{3}(4^3)-\tfrac{1}{2}(4^2)-6(4) \big) - \big(\tfrac{1}{3}(1^3)-\tfrac{1}{2}(1^2)-6(1) \big)\\ & \\ & = -\dfrac{9}{2} \; \text{m}\\ \end{aligned} \end{split}\]

It’s important to note that displacement can be negative. The way we interpret this answer is that based on the starting position of the particle, its ending position was \(9/2\) meters in the negative direction.

In order to determine the total distance, we need to separately determine the distance it travels in the positive direction and the distance it travels in the negative direction. And in order to do this, we need to determine when it’s moving in these directions. We do this with a sign chart:

Intersection Points

The only way a (continuous) velocity function can switch signs between \(+\) and \(-\), is if there is a point in the middle where it is \(=0\). These are the \(t\)-intercepts, where the velocity function intersects the horizontal axis.

We start by setting \(v(t)=0\) and solving for \(t\).

\[\begin{split} \begin{aligned} v(t) = 0 & \xrightarrow{\text{set up}} t^2-t-6=0 \\ & \\ & \xrightarrow{\text{factor}} (t-3)(t+2)=0 \\ & \\ & \xrightarrow{\text{set each factor} =0} (t-3)=0 \quad \text{or}\quad (t+2)=0\\ & \\ & \xrightarrow{\text{solve for } t} t=3 \quad \text{or}\quad t=-2\\ \end{aligned} \end{split}\]

Sign Chart

Since we’re only intersted in the time \([1,4]\), we disregard \(t=-2\) from consideration. But the other \(t\)-value, \(t=3\), is in the interval and splits it up into separate subintervals: \([1,3)\) and \((3,4]\).

We create a sign chart for \(v\) using these intervals and appropriate test numbers:

\[\begin{split} \begin{aligned} & t=2 \xrightarrow{\text{test number for } [1,3)} v(2)=(2-3)(2+2)=- \cdot + = - \\ & \\ & t=3.5 \xrightarrow{\text{test number for } (3,4]} v(3.5)=(3.5-3)(3.5+2)=+ \cdot + = + \\ \end{aligned} \end{split}\]
\[\begin{split} \begin{array}{ccc} & [1,3)& (3,4] \\ \hline v & - & + \\ \hline \text{Direction} & - \text{ Direction} & + \text{ Direction} \\ \hline \end{array} \end{split}\]

To calculate the distance traveled by the particle in the positive direction, we are going to calculate the definite integral of \(v(t)\) over the interval \((3,4]\). (This is the time interval where it is moving in the positive direction found in the sign chart.)

Since \(v(3)=0\), we can extend this interval to \([3,4]\) without changing the value we get for distance.

\[\begin{split} \begin{aligned} \left(\text{Distance in} \atop + \text{ Direction} \right) & = \int_3^4 v(t) \; dt \\ & \\ & = \int_3^4 \big(t^2-t-6 \big) \; dt \\ & \\ & = \big(\tfrac{1}{3}t^3-\tfrac{1}{2}t^2-6t \big) \bigg|_{t=3}^{t=4} \\ & \\ & = \big(\tfrac{1}{3}(4^3)-\tfrac{1}{2}(4^2)-6(4) \big) - \big(\tfrac{1}{3}(3^3)-\tfrac{1}{2}(3^2)-6(3) \big)\\ & \\ & = \dfrac{17}{6} \; \text{m}\\ \end{aligned} \end{split}\]

To calculate the distance traveled by the particle in the negative direction, we are going to calculate the definite integral of \(v(t)\) over the interval \([1,3)\). (This is the time interval where it is moving in the negative direction found in the sign chart.)

Since \(v(3)=0\), we can extend this interval to \([1,3]\) without changing the value we get for distance.

\[\begin{split} \begin{aligned} \int_1^3 v(t) \; dt & = \int_1^3 \big(t^2-t-6 \big) \; dt \\ & \\ & = \big(\tfrac{1}{3}t^3-\tfrac{1}{2}t^2-6t \big) \bigg|_{t=1}^{t=3} \\ & \\ & = \big(\tfrac{1}{3}(3^3)-\tfrac{1}{2}(3^2)-6(3) \big) - \big(\tfrac{1}{3}(1^3)-\tfrac{1}{2}(1^2)-6(1) \big)\\ & \\ & = -\dfrac{22}{3} \\ \end{aligned} \end{split}\]

Why is this integral negative? Because on this interval \([1,3)\), the velocity function is entirely negative, telling us is that during this time interval, the particle moved \(22/3 \text{ m}\) in the negative direction.

However, with total distance we want to know how much we traveled, not so much the direction we traveled in. So we make an adjustment by instead using the negative of the integral:

\[\begin{split} \begin{aligned} \left(\text{Distance in} \atop - \text{ Direction} \right) & = -\int_1^3 v(t) \; dt \\ & \\ & = -\left(-\dfrac{22}{3}\right) \; \text{m} & \\ & = \dfrac{22}{3} \; \text{m} \end{aligned} \end{split}\]

Now that we have the distance traveled in the positive direction and the distance traveled in the negative direction, we can put these together to get the total distance.

\[\begin{split} \begin{aligned} \text{Total Distance} & = \left(\text{Distance in} \atop + \text{ Direction} \right) + \left(\text{Distance in} \atop - \text{ Direction} \right) \\ & \\ & = \dfrac{17}{6} \; \text{m} + \dfrac{22}{3} \; \text{m}\\ & \\ & = \dfrac{17+44}{6} \; \text{m}\\ & \\ & = \dfrac{61}{6} \; \text{m}\\ \end{aligned} \end{split}\]

Although, not normally how we do it, we can calculate the displacement using the distance traveled in the positive direction and the distance traveled in the negative direction.

\[\begin{split} \begin{aligned} \text{Displacement} & = \left(\text{Distance in} \atop + \text{ Direction} \right) -\left(\text{Distance in} \atop - \text{ Direction} \right) \\ & \\ & = \dfrac{17}{6} \; \text{m} - \dfrac{22}{3} \; \text{m}\\ & \\ & = \dfrac{17-44}{6} \; \text{m}\\ & \\ & = \dfrac{-27}{6} \; \text{m}\\ \end{aligned} \end{split}\]

Which we see agrees with our previous result for displacement.

It is helpful to note that the calculations we have just done for displacement and total distance are very similar to the calculations we do with net area and total area. In fact, if we graph the velocity function:

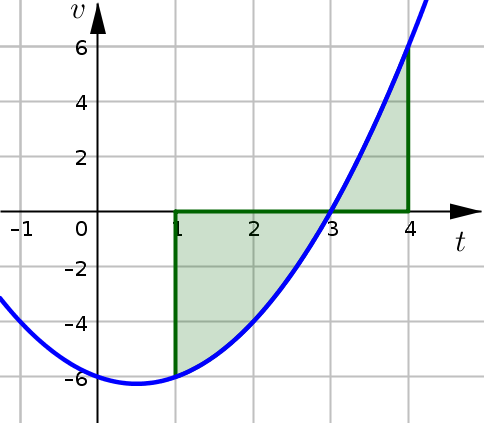
Velocity function of moving particle

and approach this problem as finding net area and total area we would see that:

\[\begin{split} \begin{aligned} & \left(\text{Area Above} \atop \text{over } [3,4]\right) \xrightarrow{\text{corresponds with}} \left(\text{Distance in} \atop + \text{ Direction} \right) \\ & \\ & \left(\text{Area Below} \atop \text{over } [1,3]\right) \xrightarrow{\text{corresponds with}} \left(\text{Distance in} \atop - \text{ Direction} \right) \\ \end{aligned} \end{split}\]

Absolute Value#

Why do we need to split up the integral when integrating this absolute value function \(\big|v(t)\big|\)? The difficulty with calculating total distance (or total area for that matter) is that the formula involves absolute value which is a piecewise defined function. To be precise:

\[\begin{split} \big|v(t)\big| = \begin{cases} v(t) \qquad & \text{if} \quad v(t)\geq 0\\ -v(t) \qquad & \text{if} \quad v(t) < 0\\ \end{cases} \end{split}\]

In order to work with the definition of this function, we need to determine where \(v(t)\) is positive and negative, which we normally do with a sign chart. Let’s consider what we did in the last example. We found the following sign chart for \(v(t)\):

\[\begin{split} \begin{array}{ccc} & [1,3)& (3,4] \\ \hline v & - & + \\ \hline \text{Direction} & - \text{ Direction} & + \text{ Direction} \\ \hline \end{array} \end{split}\]

Knowing these intervals, means we can be a little more specific about our piecewise function in this example:

\[\begin{split} \big|v(t)\big| = \begin{cases} v(t) \qquad & \text{if} \quad 3\leq t \leq 4 \\ -v(t) \qquad & \text{if} \quad 1\leq t < 3\\ \end{cases} \end{split}\]

For total distance in this last example, it really came down to integrating a piecewise function. To do this, we need to integrate over each of the pieces individually:

\[\begin{split} \begin{aligned} \left( \text{Total Distance } \atop \text{over }[1,4] \right) & = \int_1^4 \big| v(t) \big| \; dt \\ & \\ & = \underbrace{\int_1^3 \big| v(t) \big| \; dt}_{\text{Use the }-v(t)\text{ piece}} \; + \; \underbrace{\int_3^4 \big| v(t) \big| \; dt}_{\text{Use the }+v(t)\text{ piece}} \\ & \\ & = \int_1^3 \big(- v(t) \big) \; dt \; + \; \int_3^4 \big( +v(t) \big) \; dt \\ & \\ & = -\int_1^3 v(t) \; dt \; + \; \int_3^4 +v(t) \; dt \\ & \\ & = \left(\text{Distance in} \atop - \text{ Direction} \right) + \left(\text{Distance in} \atop + \text{ Direction} \right) \\ \end{aligned} \end{split}\]