(DG3) Graphically Finding Intervals of Concavity#
By the end of the lesson you will be able to:
locate the intervals of concavity given the graph of a function.
locate the inflection points given the graph of a function.
Lecture Videos#
Increasing / Decreasing#
Extreme Values#
Concavity#
Example 2#
First Derivative Rule#
Second Derivative Rule#
Examples 5 and 6#
Example 7#
Concavity#
Concave Up and Down
At \(x=c\), function \(f\) is said to be:
Concave Up: if its graph lies above the tangent line at \(x=c\).
Concave Down: if its graph lies below the tangent line at \(x=c\).
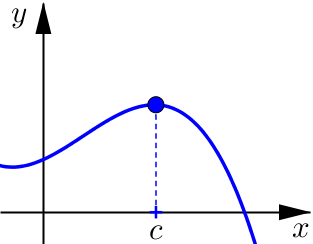
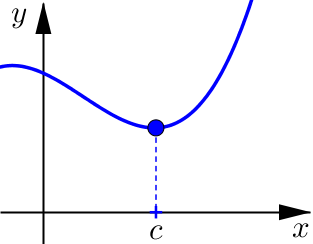
Example 1#
Determine if the following graphs are concave up or concave down at \(x=c\).
Inflection Points#
Inflection Point
An inflection point is a point on the graph where the funciton is:
continuous and
changes concavity
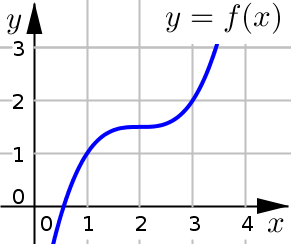
Example 2#
Use the graph of \(y=f(x)\) given below to find:
all intervals of concavity
all inflection points
Example 3#
Use the graph of \(y=f(x)\) given below to find:
all intervals of concavity
all inflection points