(DC1) Tangent Lines#

By the end of the lesson you will be able to:

  • find the slope of a secant line, the slope of the tangent line, and the equation of the tangent line at a specified point \(P\).

Lecture Videos#

Introduction to Tangent Lines#

Review of Basic Lines#

Since we are going to be discussing tangent lines, it will first be helpful to recall a few basic equations for lines in general.

Slope of a Line

The slope of the line connecting two points, \(P\) and \(Q\), is given by:

\[ m_{PQ}= \dfrac{y_Q-y_P}{x_Q-x_P} \]
Point-Slope Formula

The equation of a line with slope \(m\) and point \((x_c, y_c)\) is given by:

\[ y-y_c = m(x-x_c) \]

Notice: In order to define a line, we need to know 2 points on the line (so that we can find the slope).

Circles#

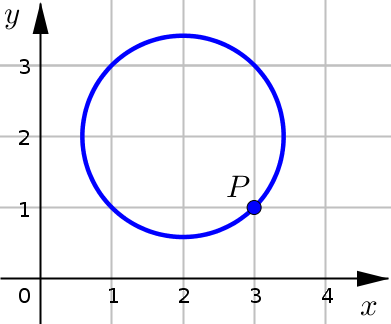
We begin by considering the case of the tangent line at a point \(P\) on a circle. Intuitively, we have some idea what this tangent line should look like.

What are some important characteristics we would want the tangent line to have?

  1. It should just barely touch the circle at point \(P\).

  2. Very close to point \(P\), the tangent line should give a good approximation of the circle at \(P\).

Circle
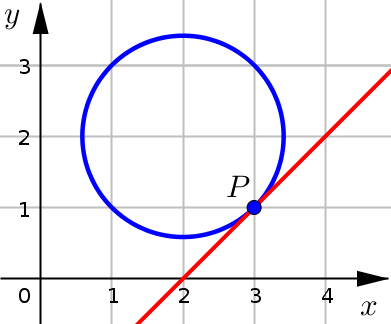
Tangent line to circle
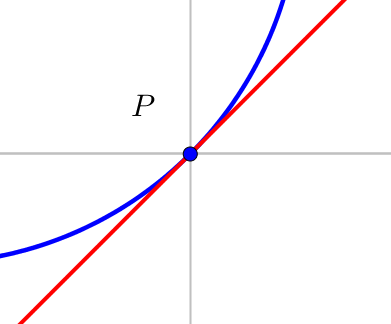
Zoomed-in at the point of tangency

Notice that when we zoom in at point \(P\):

  • the circle and the tangent line have the same slope (direction) and

  • we can barely tell the difference between the line and the circle.

Constructing a Tangent Line#

Once we’ve decided on what characteristics the tangent line should possess, the question becomes: How do we actually construct the tangent line at point \(P\)?

The difficulty here is that it takes \(2\) points to define a line, but we want our tangent line to only touch the circle or curve at \(1\) point.

As we are going to see, the construction technique involves secant lines and limits:

  1. Pick a point \(Q\) on the curve which is close to \(P\).

  2. Draw a secant line connecting points \(P\) and \(Q\).

  3. Calculate the limit as point \(Q\) approaches point \(P\).

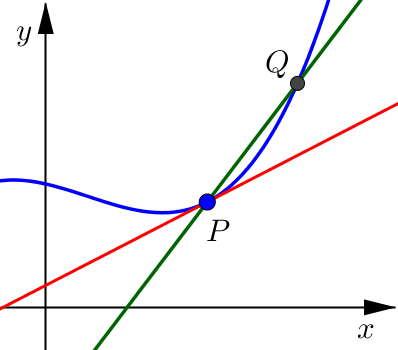
Secant Line
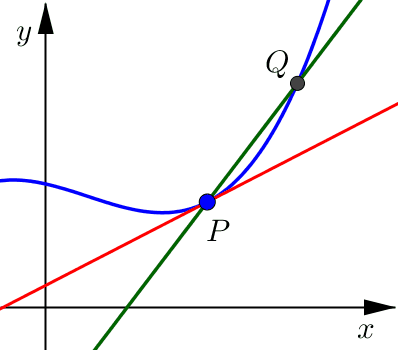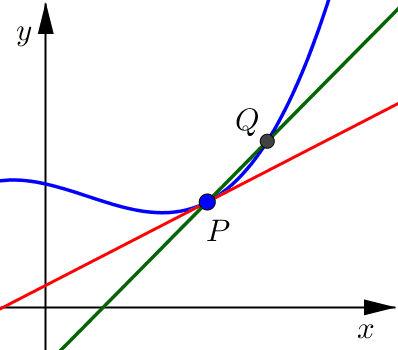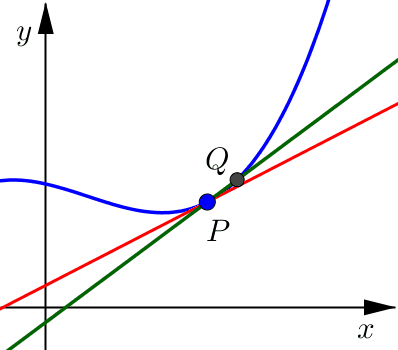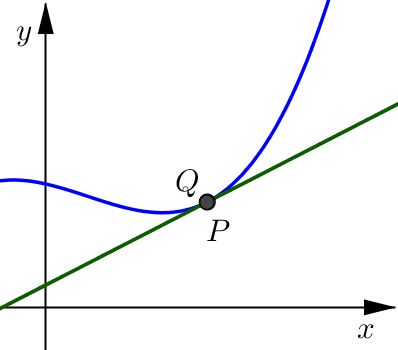
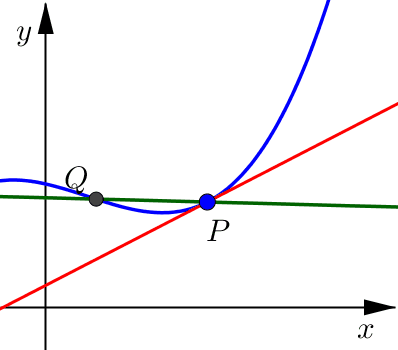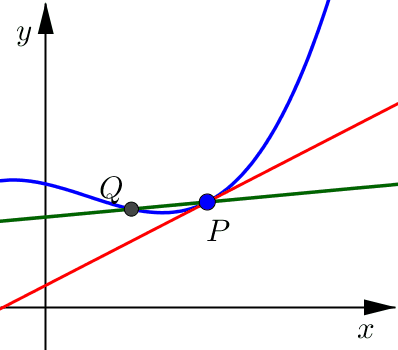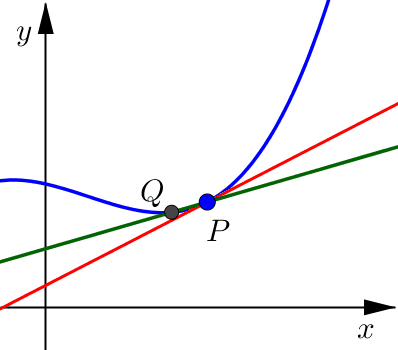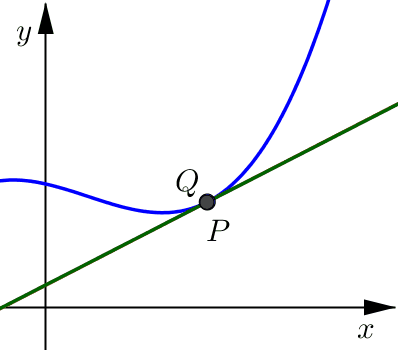
Table of Function Values
Table of Function Values

Notice that as this point \(Q\) moves closer and closer to point \(P\), from either the right or the left side, the secant line looks more and more like what we would want for the tangent line.

Once \(Q\) is very, very close to \(P\) the secant line and the tangent line are indistinguishable. Both lines include point \(P\) and have a very similar slope (essentially they are pointing in almost the same direction).

Slope of the Tangent Line#

Since we’ve noticed that as point \(Q\) gets closer and closer to point \(P\) (our point of tangency), the slope of the secant line gets closer and closer in value to the slope of the tangent line.

Well, we’ve introduced all the necessary machinary to rigorously deal with this idea of getting closer and closer: limits.

Slope Formula

\[ m= \lim_{x\to a} \dfrac{f(x)-f(a)}{x-a} \]

Slope Formula (Better)

\[ m= \lim_{h\to 0} \dfrac{f(a+h)-f(a)}{h} \]
Interpretation of Formula

Slope of the Tangent Line is what we are calculating and is denoted by \(m\).

Slope of the Secant Line connecting points \(P\) and \(Q\) is given by both fractions:

\[ \tfrac{f(x)-f(a)}{x-a}\text{ or } \tfrac{f(a+h)-f(a)}{h} \]

Point \(Q\) approaches point \(P\) by calculating the limit.

Graph of Secant and Tangent Lines
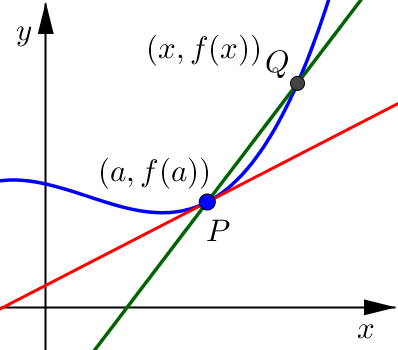
Horizontal Asymptote
How are these two slope formulas equivalent?

In the first formula, we have the coordinates of point \(Q\) written as \((x,f(x))\). Instead, we can think of \(Q\) as being close to point \(P\) but shifted slightly to the left or right.

If we start with point \(P(a,f(a))\) and slightly shift the \(x\)-coordinate by a small amount we would get \(x=a+h\) (where we use \(h\) to represent how much we are shifting by). Using this \(x\)-coordinate for point \(Q\) gives us \(Q(a+h, f(a+h))\)

Using these slightly revised coordinates in the slope formula we get:

\[ m_{PQ}= \dfrac{y_Q-y_P}{x_Q-x_P}=\dfrac{f(a+h)-f(a)}{(a+h)-a} = \dfrac{f(a+h)-f(a)}{h} \]

Example 1#

Consider the parabola \(y=x^2\) and point \(P(1,1)\).

(a) What is the slope of the secant line \(PQ\) for \(Q(2,4)\)?

Remember that the slope of a line is: change in \(y\) divided by the change in \(x\).

\[ m_{PQ}= \dfrac{y_Q-y_P}{x_Q-x_P}=\dfrac{4-1}{2-1} = 3 \]
(b) What is the slope of the secant line \(PR\) for point \(R\) at \(x=1.1\)?

In order to calculate the slope of this secant line, we first need to determine the \(y\)-coordinate for point \(R\). We do this by plugging the \(x\)-value into the function:

\[ x=1.1 \longrightarrow y_R = (1.1)^2 = 1.21 \]

Once we have all of the necessary coordinates for both points, we go to the basic slope formula:

\[ m_{PR}= \dfrac{y_R-y_P}{x_R-x_P}=\dfrac{1.21-1}{1.1-1} = \dfrac{0.21}{0.1}=2.1 \]
(c) What is the slope of the tangent line to this parabola at point \(P\)?

Since point \(P\) has coordinates \((1,1)\), the \(x\)-coordinate tell us the \(a\)-value to use in our slope calculations: \(a=1\).

To get started, we should write down the tangent slope formula and then do the necessary evaluations.

\[\begin{split} m & = \lim_{x\to 1} \dfrac{f(x)-f(1)}{x-1} \\ &\\ & = \lim_{x\to 1} \dfrac{x^2-(1)^2}{x-1} \\ \end{split}\]

This is an indeterminate form, so we need to use our algebraic methods to calculate this limit. In this case, factor and cancel:

\[\begin{split} & = \lim_{x\to 1} \dfrac{(x-1)(x+1)}{(x-1)} \\ &\\ & = \lim_{x\to 1} (x+1) \\ \end{split}\]

And now we have a polynomial in terms of \(x\), so we can use direct evaluation to finish our calculations:

\[\begin{split} & = 1+1 \\ &\\ & = 2 \\ \end{split}\]

Example 2#

Find an equation of the tangent line to the hyperbola \(y=\dfrac{3}{x}\) at the point \(P(3,1)\).

Click through the tabs to see the steps of our solution.

Since we want to find the equation of the tangent line, let’s start with the point-slope formula for the equation of a line:

\[ y-y_c=m(x-x_c) \]

This tells us we need three things, \(x\)-coordinate: \(x_c\), \(y\)-coordinate: \(y_c\), and slope \(m\). For a tangent line:

  • \(x_c = a\)

  • \(y_c = f(a)\)

  • \(m = f'(a) = \displaystyle \lim_{h\to 0} \dfrac{f(a+h)-f(a)}{h} \)

We are explicitly given the \(x\) and \(y\) coordinates for point \(P(3,1)\).

\[ x_c=3 \qquad y_c=1 \]

In case we weren’t given \(y_c\) we could actually calculate this by evaluating the function:

\[ y_c = f(x_c) = f(3) = \dfrac{3}{3}=1 \]

First thing we want to do is write down the tangent slope formula:

\[\begin{split} m & = \lim_{h\to 0} \dfrac{f(3+h)-f(3)}{h} \\ &\\ & = \lim_{h\to 0} \dfrac{\tfrac{3}{3+h}-\tfrac{3}{3}}{h} \\ \end{split}\]

Instead of have these multiple fractions stacked on top of each other, its helpful to rewrite this as a product:

\[\begin{split} & = \lim_{h\to 0} \dfrac{1}{h}\cdot \left[\dfrac{3}{3+h}-1\right] \\ \end{split}\]

Next we work on getting a common denominator for those two terms inside the brackets, so that we can actually combine them into one fraction by doing the subtraction.

\[\begin{split} & = \lim_{h\to 0} \dfrac{1}{h}\cdot \left[\dfrac{3}{3+h}-\dfrac{3+h}{3+h}\right] \\ &\\ & = \lim_{h\to 0} \dfrac{1}{h}\cdot \left[\dfrac{3-(3+h)}{3+h}\right] \\ &\\ & = \lim_{h\to 0} \dfrac{1}{h}\cdot \left[\dfrac{-h}{3+h}\right] \\ \end{split}\]

At this point though we still have a \(0/0\)-indeterminate form, but we can now cancel the h’s.

\[\begin{split} & = \lim_{h\to 0} \dfrac{-1}{3+h} \\ \end{split}\]

And now we have a rational function in terms of \(h\), so we can use direct evaluation to finish our calculations:

\[\begin{split} & = \dfrac{-1}{3+0} \\ &\\ & = \dfrac{-1}{3} \\ \end{split}\]

Now we just need to plug all of the pieces into the point-slope equation for our line:

\[ y-y_c=m(x-x_c) \]

We have found:

  • \(x_c = 3\)

  • \(y_c = 1\)

  • \(m = -\tfrac{1}{3} \)

Giving us the tangent line equation:

\[ y-1=-\dfrac{1}{3}(x-3) \]

Or solving for \(y\):

\[ y= -\dfrac{1}{3}x+2 \]