(DC4) Differentiability#

By the end of the lesson you will be able to:

  • determine where a function is differentiable given a graph or formula of the function and explain why.

Lecture Videos#

Differentiability#

Differentiability (Precise)

A function \(f\) is differentiable at \(x\) provided the following limit exists.

\[ \lim_{h\to 0} \dfrac{f(x+h)-f(x)}{h} \]

Otherwise if the limit does not exist, \(f\) is said to be nondifferentiable at \(x\).

Domain of the Derivative#

Function: \(f'\) is a brand new function derived from \(f\).

Variable: If \(x\) is the variable of \(f\), then \(x\) is also the variable of \(f'\).

  • Note that \(f'\) does not depend on \(h\). When we calculate the limit, all \(h\) terms should disappear once we finish.

Domain: The domain of \(f'\) \(=\) all \(x\)-values in the domain of \(f\) where the above limit exists. Note that the domain of \(f'\) may be smaller than the domain of \(f\).

Example 1#

State the domain of the function \(f\) and its derivative \(f'\).

\[ f(x)=\sqrt{x} \qquad \text{and}\qquad f'(x)=\dfrac{1}{2\sqrt{x}} \]

Click to go through our solutions and explanation for this example.

The domain of the function \(f(x)=\sqrt{x}\) is the interval \([0,\infty)\)

  • Remember that the square root function is undefined for negative numbers.

The domain of the derivative \(f'(x)=\tfrac{1}{2\sqrt{x}}\) is the interval \((0,\infty)\).

We can see this directly from the limit definition:

\[\begin{split} \lim_{h\to 0^+}\dfrac{f(0+h)-f(0)}{h} &= \lim_{h\to 0^+}\dfrac{\sqrt{0+h}-\sqrt{0}}{h} \\ & \\ & = \lim_{h\to 0^+}\dfrac{\sqrt{h}}{h} = \lim_{h\to 0^+}\dfrac{1}{\sqrt{h}} = \infty \\ \end{split}\]

Since this limit technically does not exist, the function \(f\) is nondifferentiable at \(x=0\).

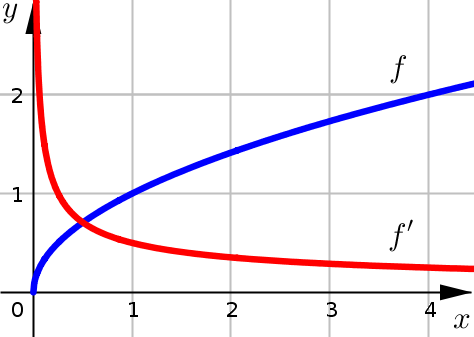
Vertical Tangent

Notice that in the graph of \(f\) and \(f'\) we see:

  • \(f'\) has a vertical asymptote at \(x=0\)

  • \(f\) looks like it has a vertical tangent line at \(x=0\).

Try zooming-in on the graph of \(f\) near \(x=0\). You should be able to tell that the graph looks close to being a vertical line there.

Slope of the Curve#

Slope of the Curve

The slope of the curve at point \(P\) is defined to be the slope of the tangent line to the curve at\(P\).

  • Recall that the tagent line is the straight line that gives the best linear approximation of the curve at point \(P\).

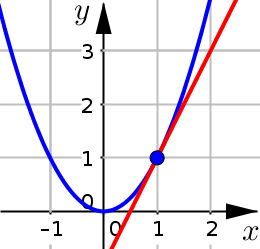
Parabola and Tangent Line
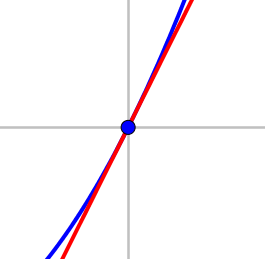
Parabola and Tangent Line Zoomed In

Notice that when you zoom in on point \(P\), the curve actually does look like a straight line near \(P\).

At point \(P\), the curve and tangent line are going in the same direction (have the same slope).

Differentiability#

Differentiability (Graphical)

A function is differentiable provided its graph does not have any abrupt changes or vertical tangents.

Abrupt Changes: What constitutes an abrupt change?

  • jump or break in the graph of \(f\)

  • sudden changes in the slope of \(f\).

Examples of Nondifferentiability#

Each of the following functions is nondifferentiable at \(x=2\).

Each of the following graphs are continuous at \(x=2\), but nondifferentiable there.

Cusp

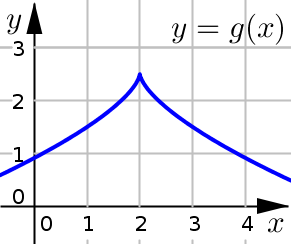
Example of a cusp or corner. Note the abrupt change in the slope between the left and right side.

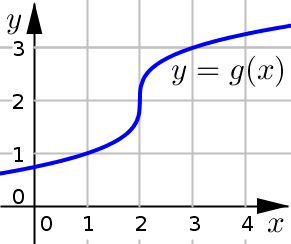
Vertical Tangent

Example of a vertical tangent. Small changes in the input result in large changes in the output.

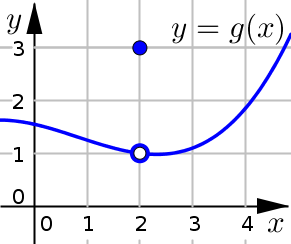
Removeable Discontinuity

Removeable Discontinuity (hole)

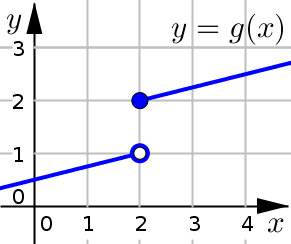
Jump Discontinuity

Jump Discontinuity

Infinite Jump Discontinuity

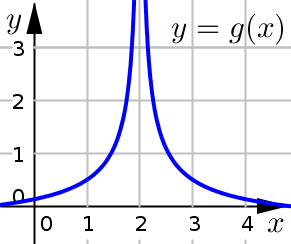
(Infinite) Jump Discontinuity

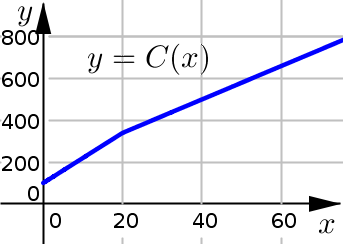
Example 2#

Determine whether the following function is differentiable at \(x=20\).

\[\begin{split} C(x)=\begin{cases} 100+12x & \quad \text{if} \quad 0\leq x \leq 20 \\ 180+8x & \quad \text{if} \quad x > 20\\ \end{cases} \end{split}\]

Click to go through our solutions and explanation for this example.

In order to determine the differentiability of the function \(C\) at \(x=20\), we need to show that the following limit exists:

\[ \lim_{h\to 0} \dfrac{C(20+h)-C(20)}{h} \]

Since this is a piece-wise function which splits at \(x=20\), we need to calculate the left and right side limits.

Let’s start by calculating the left-side limit

\[ \lim_{h\to 0^-} \dfrac{C(20+h)-C(20)}{h} \]

Because we have a piece-wise function, we need to determine which piece to use when evaluating \(C(20+h)\) and \(C(20)\).

Which piece to use when \(x=20\)? Looking at the inequalities in the definition of \(C\) we see that \(0\leq x\leq 20\) accounts for the case \(x=20\). This means we need to use the \(100+12x\) piece.

\[ C(20)=100+12(20) = 340 \]

What about when \(x=20+h\)? Since \(h\) is approaching \(0\) from the left, this means the \(h\) values we’re using are close to \(0\) but slightly negative. Which makes the expression \({20+h}\) slightly smaller than \(20\). Since \(20+h<20\), this means we need to use the \(100+12x\) piece.

\[ C(20+h)=100+12(20+h) = 100 + 240 +12h = 340+12h \]

Using these in our limit we get:

\[\begin{split} \lim_{h\to 0^-} \dfrac{C(20+h)-C(20)}{h} & = \lim_{h\to 0^-} \dfrac{340+12h-340}{h} \\ & \\ & = \lim_{h\to 0^-} \dfrac{12h}{h} = \lim_{h\to 0^-} 12 = 12 \\ \end{split}\]

Next we need to calculate the right-side limit

\[ \lim_{h\to 0^+} \dfrac{C(20+h)-C(20)}{h} \]

Previously, we found \(C(20)=340\).

What about piece should we use for \(C(20+h)\)? Since \(h\) is approaching \(0\) from the right, this means the \(h\) values we’re using are close to \(0\) but slightly positive. Which makes the expression \({20+h}\) slightly larger than \(20\). Since \(20+h>20\), this means we need to use the \(180+8x\) piece.

\[ C(20+h)=180+8(20+h) = 180 + 160 +8h = 340+8h \]

Using these in our limit we get:

\[\begin{split} \lim_{h\to 0^+} \dfrac{C(20+h)-C(20)}{h} & = \lim_{h\to 0^+} \dfrac{340+8h-340}{h} \\ & \\ & = \lim_{h\to 0^+} \dfrac{8h}{h} = \lim_{h\to 0^+} 8 = 8 \\ \end{split}\]

Since the left and right sides are not equal to each other, we can conclude that the overall limit:

\[ \lim_{h\to 0} \dfrac{C(20+h)-C(20)}{h} \quad \text{DNE} \]

Since this limit does not exist, we can conclude that this funciton is nondifferentiable at \(x=20\). Notice that we can also see this in the graph of the function. There is a noticeably abrupt change in the slope of the curve there; identifiable as a corner in the graph.

Continuous Function

Differentiability and Continuity#

Theorem

If \(f\) is differentiable at \(x=a\), then \(f\) is also continuous at \(x=a\).

This theorem tells us a few things:

  1. Every differentiable function is continuous.

  2. If \(f\) is discontinuous at \(x=a\), then \(f\) is nondifferentiable at \(x=a\).

Danger

Even though every differentiable function is guaranteed to be continuous, the opposite is not true in general: Knowing that a function is continuous is not enough to guarantee that it is differentiable.

See the last example for a function that is continuous at \(x=20\), but nondifferentiable there.

Example 3#

Determine whether the following function is continuous and differentiable at \(x=15\).

\[\begin{split} C(x)= \begin{cases} 200+2x & \text{for}\quad 0\leq x\leq 15 \\ 400+2x & \text{for}\quad 15< x\leq 30 \\ 600+2x & \text{for}\quad 30< x\leq 45 \\ \end{cases} \end{split}\]

Click through the tabs to see the steps of our solution.

Since differentiating a function is generally more involved (especially for piece-wise functions). Let’s start by first checking whether this function is continuous at \(x=15\).

To check continuity, we need to compute the left side limit, right side limit, the function value, and then check that these values are equal.

We want to calculate the left side limit:

\[ \lim_{x\to 15^-} C(x) \]

Since \(x\) is approaching \(15\) from the left, this means \(x\) is close to \(15\), but slightly smaller. Therefore \(x<15\), which means we should use the \((200+2x)\) piece:

\[ \lim_{x\to 15^-} C(x) = \lim_{x\to 15^-} (200+2x) = 200 + 2(15) = 230 \]

(Which we can do by direct evaluation, because \((200+2x)\) is a polynomial.)

We next need calculate the right side limit:

\[ \lim_{x\to 15^+} C(x) \]

Since \(x\) is approaching \(15\) from the right, this means \(x\) is close to \(15\), but slightly larger. Therefore \(x<15\), which means we should use the \((400+2x)\) piece:

\[ \lim_{x\to 15^+} C(x) = \lim_{x\to 15^+} (400+2x) = 400 + 2(15) = 430 \]

(Which we can do by direct evaluation, because \((400+2x)\) is a polynomial.)

Since the left and right sides are not equal to each other, we can conclude that the overall limit:

\[ \lim_{x\to 15} C(x) \quad \text{DNE} \]

Since the overall limit does not exist we can conclude that the function is discontinuous at \(x=15\)

By the theorem relating differentiability and continuity, we are then able to also conclude that the function is nondifferentiable at \(x=15\) as well.